📌 강의 목차
00:00 도입부
00:23 Data Description
02:29 평균의 개념
03:51 평균, 중앙값, 최빈값
05:51 히스토그램과 도수분포표
07:23 히스토그램과 밀도함수(Density Plot)
09:19 분산에 따른 평균 해석
11:02 Percentile
12:57 Percentile 사례 분석 (1)
15:29 Percentile 사례 분석 (2)
17:48 요약값과 분포의 시각화
18:45 Boxplot(상자그림)
20:29 확률 나타내기
🗒️ 요약 노트
데이터의 특성과 모양을 요약하여 기술하는 방법
Data Description/Data Profiling
중심 경향 : 주어진 데이터를 대표하는 값을 찾는 것
- 평균(Mean)
- 중앙값(Median)
- 최빈값(Mode)
퍼진 정도
- 범위(Range)
- 분산(Variance)
- 표준편차
- Percentile
퍼진 모양(대칭) : 데이터의 분포 정도가 어느 쪽으로 치우쳤는지 확인하는 것
- 왜도(Skewness)
히스토그램
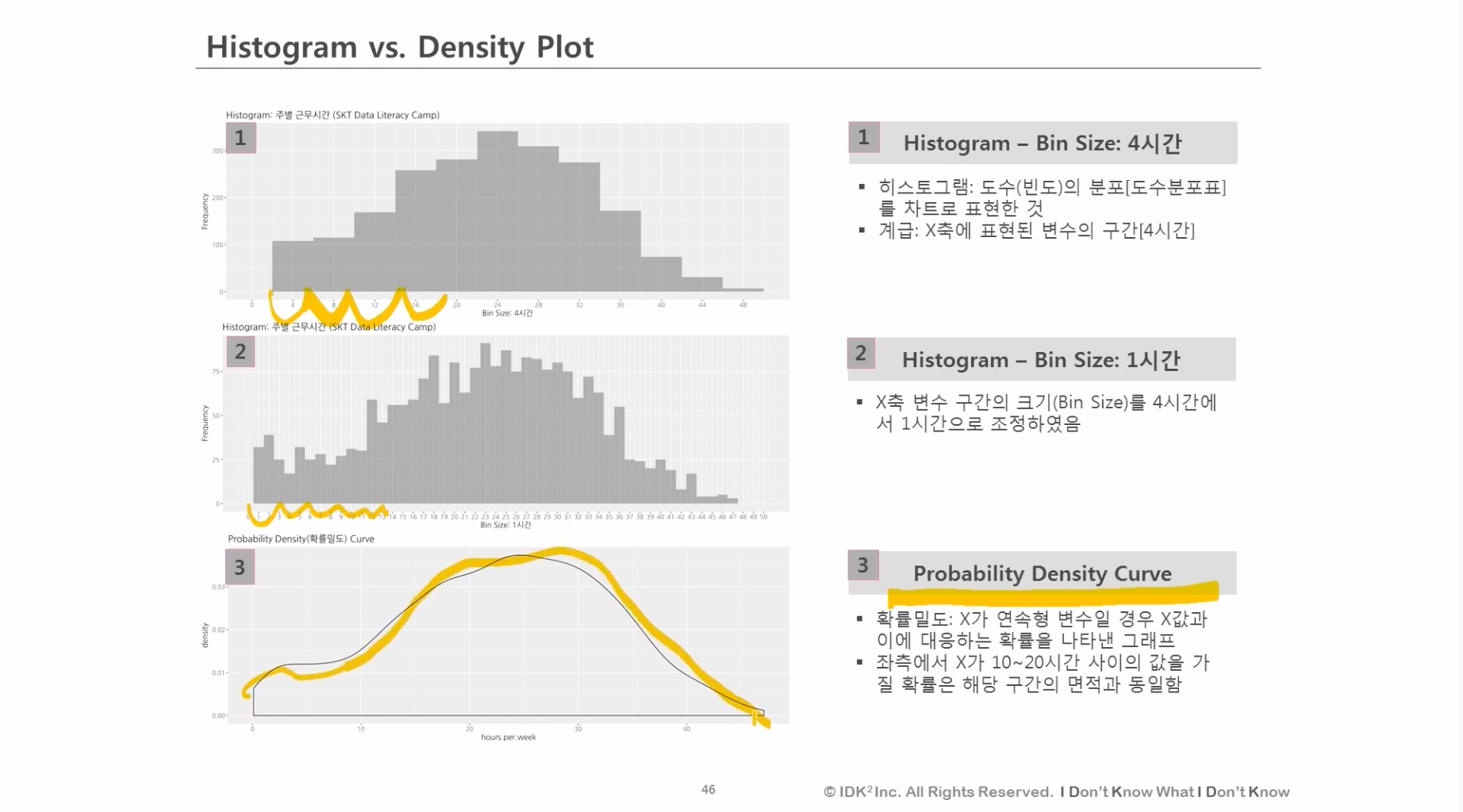
히스토그램이란? 연속형 데이터를 사용자 지정 범위로 응축하여 분포를 나타내는 것. 많은 양의 데이터를 그래프로 요약하여 보다 효율적으로 정보를 전달할 수 있음.
히스토그램의 용도 대량의 데이터를 요약하고 데이터의 분포 추세(데이터의 간격, 중앙값, 최빈값, 특이치 등 확인)을 확인해야 할 때 유용합니다.
막대 그래프(Bar chart)와의 차이점
- 막대 그래프는 범주형(category) 데이터를 표현하는데 주로 사용됩니다. 개별 막대가 서로 분리되어 있으며 각각의 수량의 크기를 나타냅니다.
- 히스토그램은 측정된 연속적인 값을 데이터로 표현하는데 주로 사용됩니다. 개별 막대의 간격이 없으며 순서를 임의로 바꿀 수 없습니다. 개별 막대(구간)의 크기를 직접 정할 수 있으며 막대의 크기(너비)는 일정해야 합니다.
Percentile
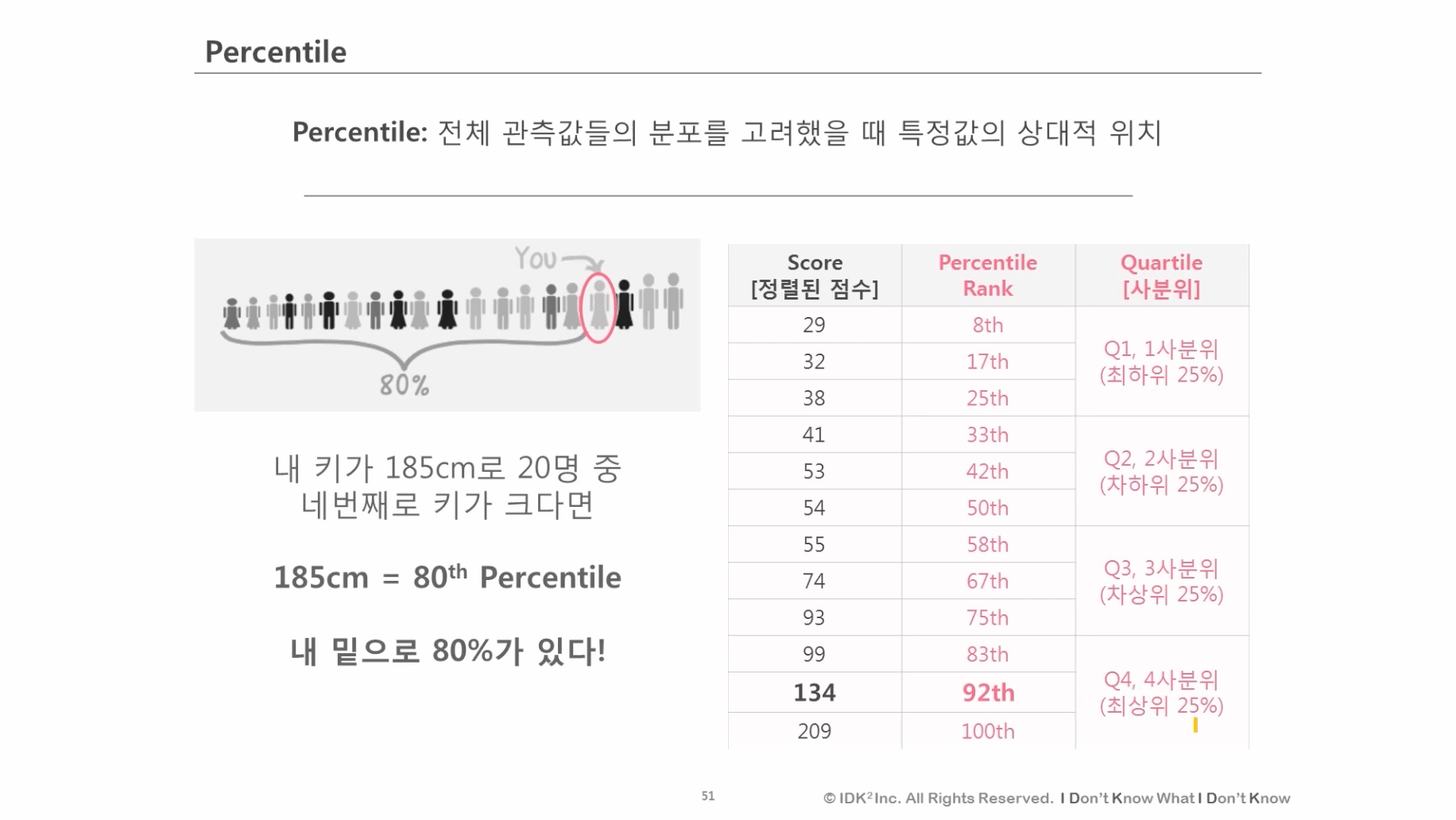
1사분위, 2사분위와 같이 특정값의 상대적 위치를 표현한 값. Percentile을 함으로써 숫자 데이터를 분류/구분할 수 있으며 새로운 패턴을 찾아낼 수도 있습니다.
Boxplot(상자수염그림)
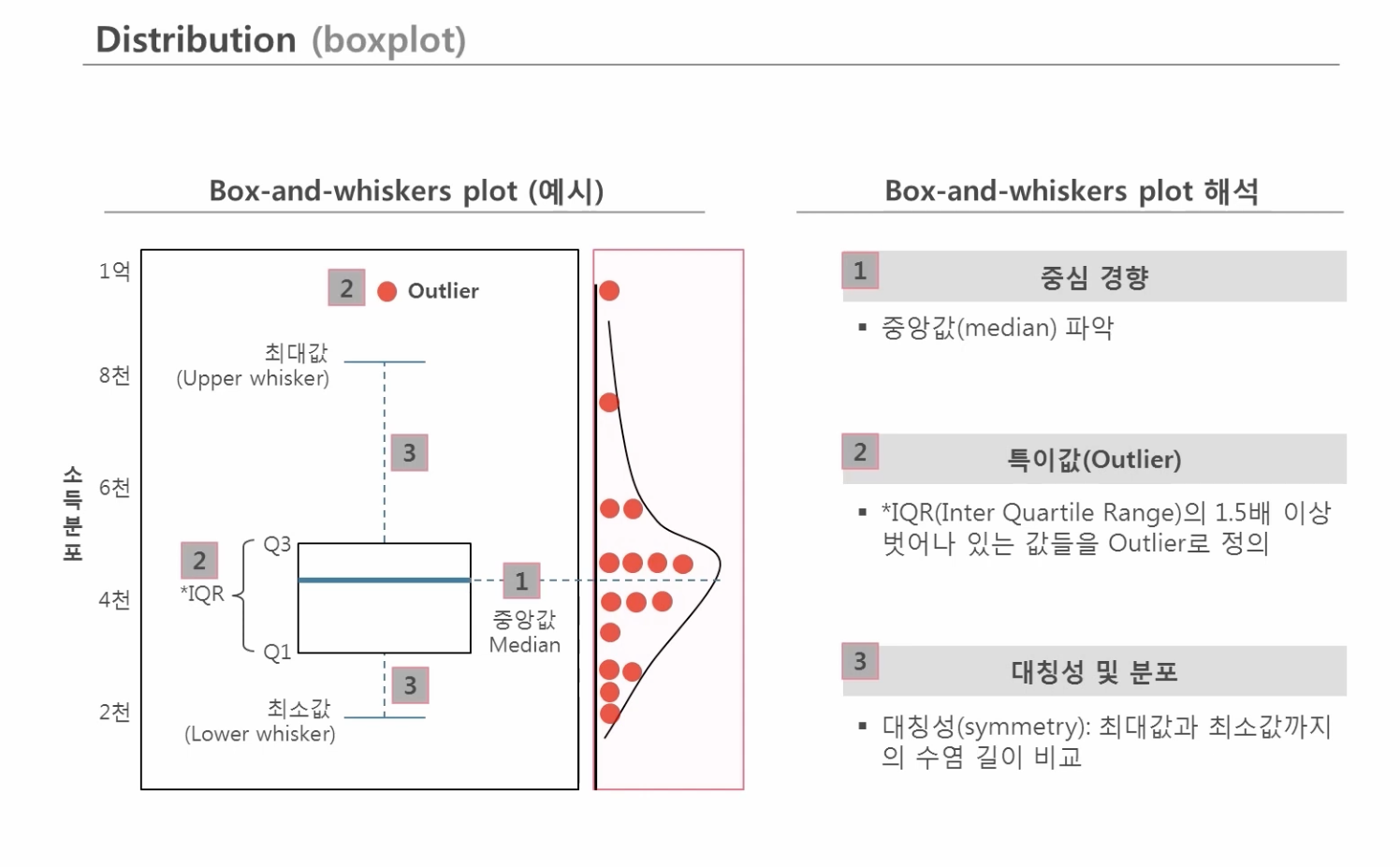
데이터의 분포를 나타내는 가장 대표적이고 효과적인 방법. 상자(Q1;1사분위~Q3;3사분위 구간)와 수염(최소값과 최대값의 위치)을 통해 중심 경향, 특이값(Outlier), 대칭성 및 분포를 확인할 수 있습니다.
📖 강의 교재
💡 관련 아티클


🗣 후기 이벤트
학습 콘텐츠가 도움이 되셨나요? 블로그에 후기를 작성해보세요.
블로그에 하트카운트 학습 콘텐츠와 관련된 글을 작성 후 아래 폼을 제출해주시면, 추첨하여 네이버페이 5,000원 쿠폰을 전달드립니다. 내가 공부한 내용을 기록하고, 다른 사람들에게 추천해보세요.
![[무료 강의] EDA 101 (2): 데이터의 모양 묘사하기 (히스토그램, boxplot, percentile)](/ko/content/images/size/w2000/2024/04/-----------------------_-002--3-.png)

![[무료 강의] EDA 101 (1): 분석하기 좋은 데이터셋, 변수 유형별 시각화 방법](/ko/content/images/size/w360/2024/04/-----------------------_-001--6-.png)
![[무료 강의] EDA 101 (3): 평균의 함정, 시각화 기본 문법, 상관 관계 분석](/ko/content/images/size/w360/2024/04/-----------------------_-002--5-.png)




![[Monthly Webinar] 11. 데이터 보고서 잘 쓰기](/ko/content/images/size/w540/2023/11/---------------_11-----1-.png)