매체별 광고비가 매출에 미치는 영향, 회귀분석 사례

오늘은 변수 간의 관계를 통계적으로 설명하는 알고리즘인 회귀분석에 대해 알아보겠습니다.

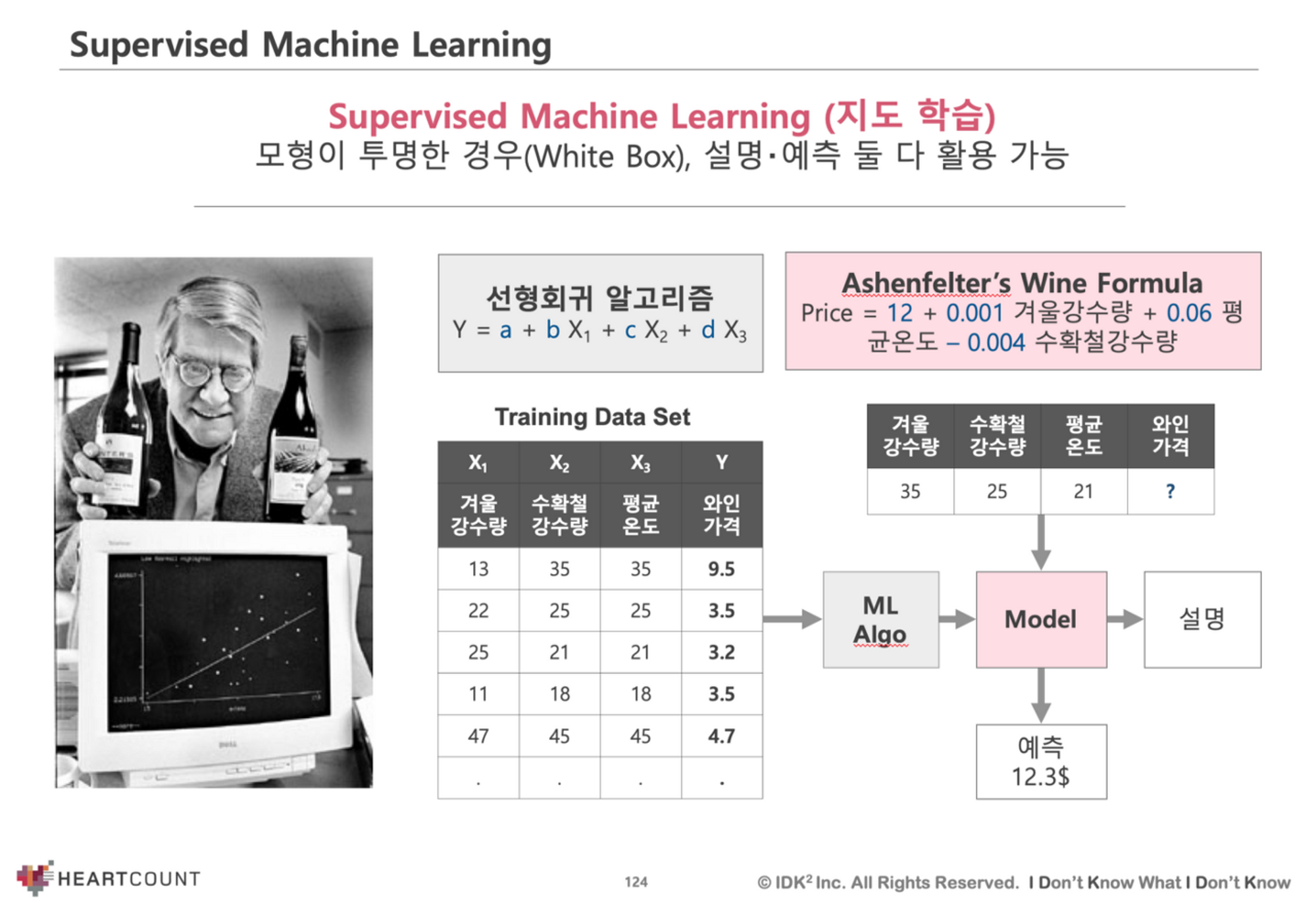
선형회귀 (Linear Regression) 분석

• 변수값(매출, 만족도 등)의 차이가 어디에서 비롯되는지 알고자 할 때 사용하는 가장 오래되고 널리 쓰이는 이해하기 쉬운 알고리즘

• 독립변수(X)를 가지고 숫자형 종속변수(Y)를 가장 잘 설명‧예측(Best Fit)하는 선형 관계(Linear Relationship)를 찾는 방법

• 앞으로 100년 후에도 꾸준히 사용될 알고리즘으로 선형회귀 분석이 첫번째로 꼽히는 이유는 모형의 내용을 사람이 직관적으로 이해할 수 있기 때문

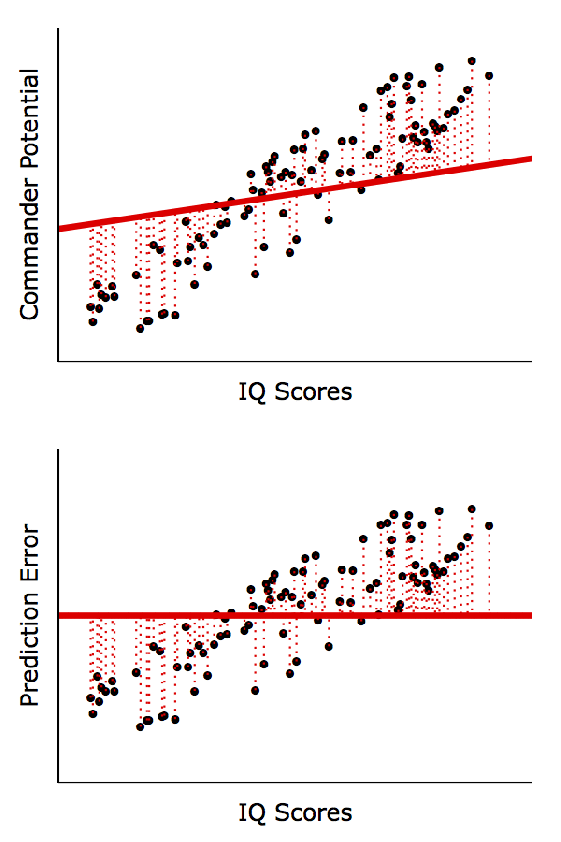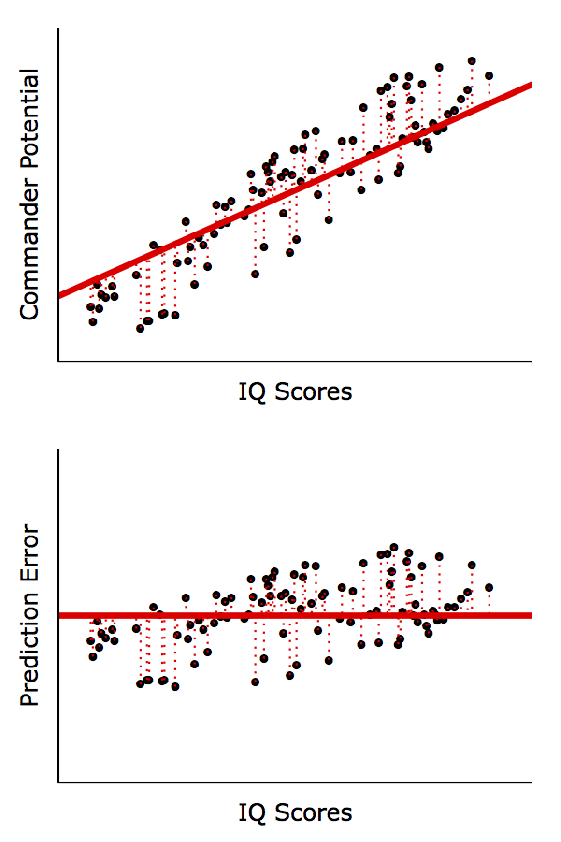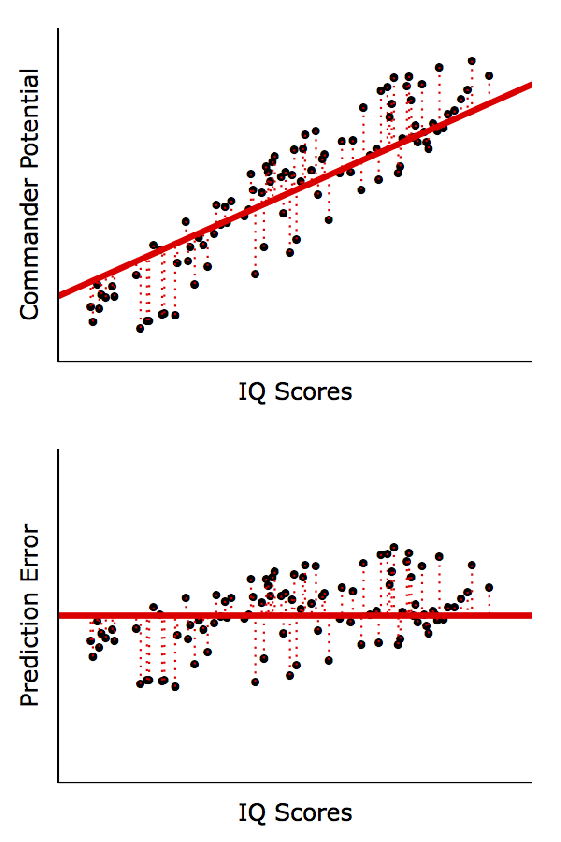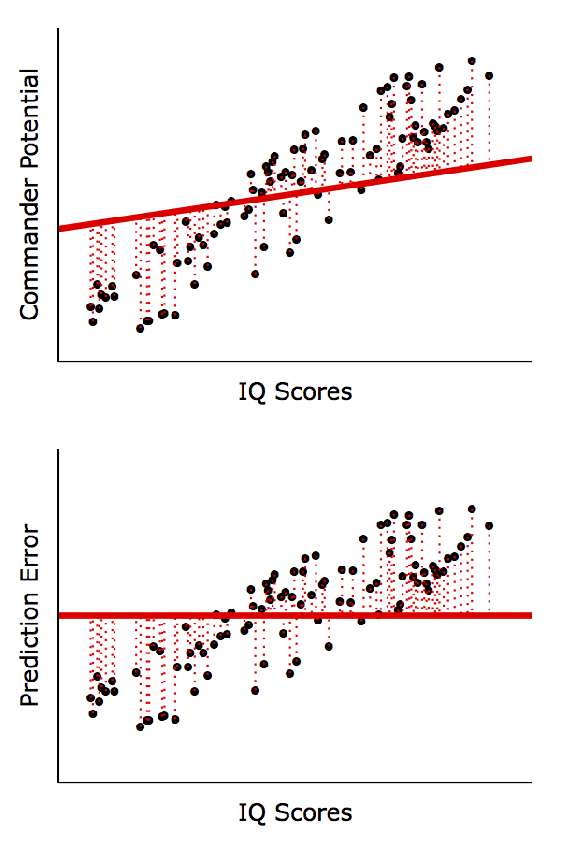
선형회귀분석 계산방법 (Least Squares)

X와 Y 사이에 선형적 관계가 있다는 가정 하에 실제 Y값(점들)과 예측한 Y값(직선)의 차이를 최소화하는 방정식을 계산

⎮Y = b0 + b1X + error

• b0 : Y축 절편(Intercept); 예측변수가 0일 때 기대 점수를 나타냄

• b1 : 기울기로 X가 한 단위 증가했을 때의 Y의 평균적 변화값을 나타냄

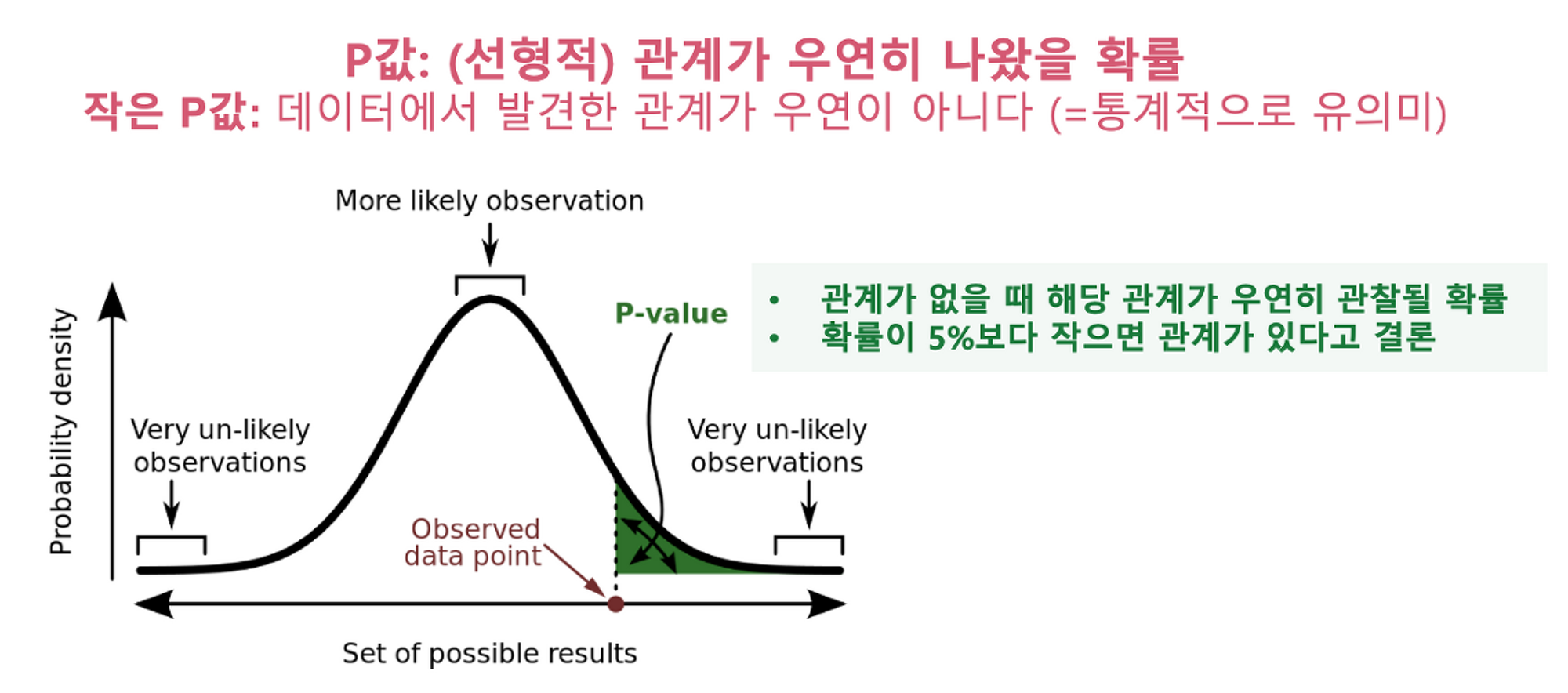
P-Value (Probability-Values)

• Statistical Significance(통계적 유의성)을 나타내는 수치로 X와 Y 사이에 발견된 관계가 통계적으로 유의미한지 여부를 알려줌

• 데이터를 통해 확인한 관계가 우연히 나왔을 확률로 생각하면 됨

• P값이 0.03이라면 X와 Y 사이에 (선형적) 관계가 없는데도 불구, 데이터 샘플링의 실수로 관계가 우연히 발생했을 확률이 3% 정도 된다는 이야기

• 절대적 기준은 없고 통상 0.01~0.05 보다 낮으면 유의미하다고 봄

• 변수 사이 관계의 세기(Size of an Effect)를 나타내는 것은 아님 (P값은 0.0001로 매우 작지만 X의 변화에 따른 Y값의 변화[관계의 세기]는 무의미한 수준으로 미미할 수 있음)

R2 (R-SQUARED; 결정계수)

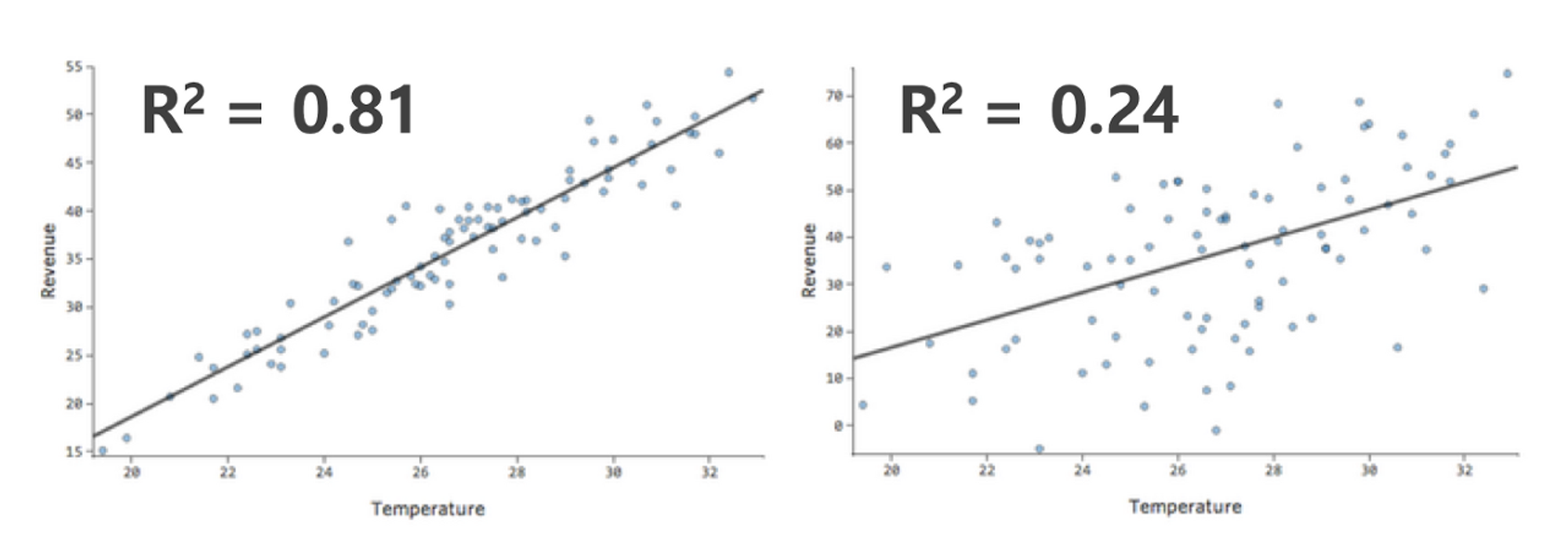
• X가 Y를 얼마나 잘 설명/예측하는가를 알려주는 통계량

• Goodness of Fit: X로 설명할 수 있는 Y 변화량의 크기를 나타내며 0에서 1사의 값을 가짐 (1이면 차이를 100% 설명한다는 이야기)

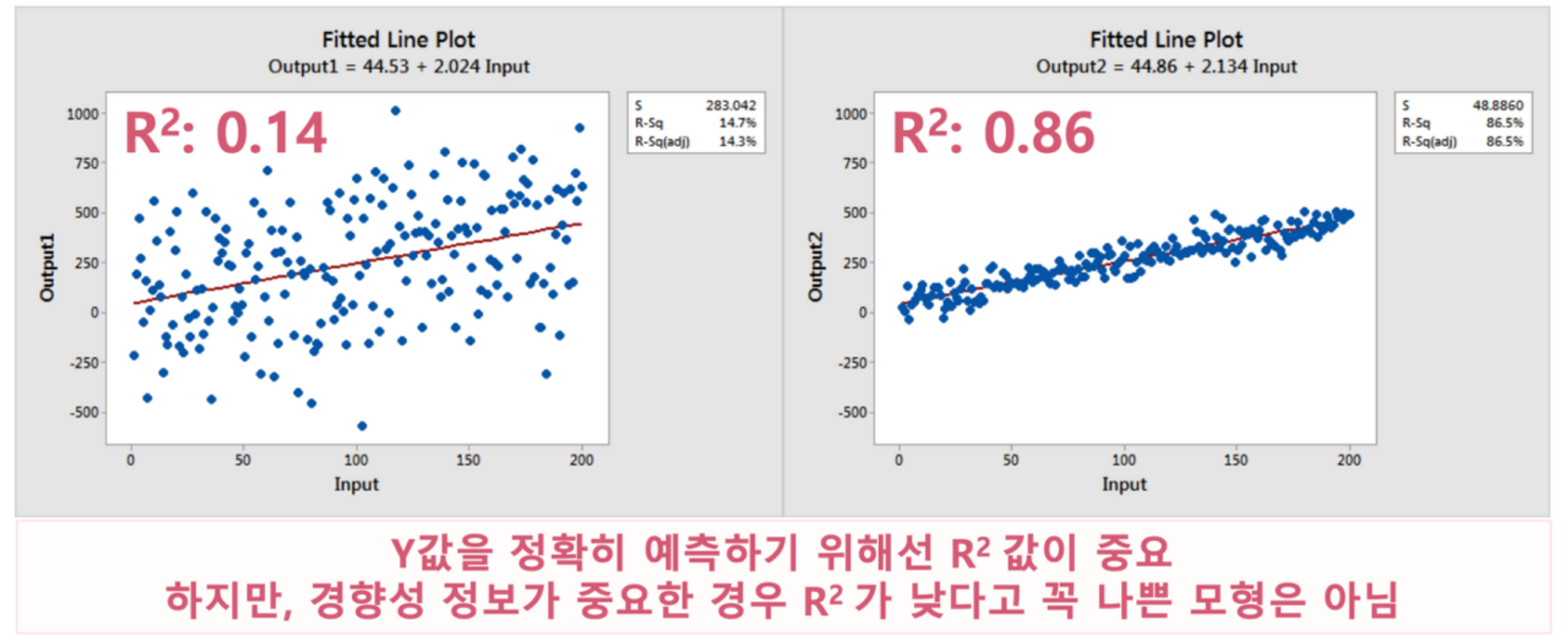
• 아래 그림처럼 낮은 결정계수가 반드시 나쁜 (Inherently Bad) 것은 아님
◦ 좌, 우 모두 동일한 회귀방정식: Y = 44 + 2*X; P < 0.001
◦ 우측 모형이 좌측 모형보다 예측 정확도(R2)는 매우 높음
(즉, X값이 250이면 Y값은 얼마가 될까를 더 정확히 예측)
◦하지만, 변수 간 경향성은 동일: X: 1단위 증가 → Y: 2단위 증가
(예측의 정확도가 아니라 경향성을 파악하는 게 중요하다면 좌, 우 모두 유의미한 패턴임)

Analysis in HEARTCOUNT: 회귀분석 실습

Dataset

4개의 광고 매체와 매출이 담겨 있는 데이터셋으로 간단한 회귀분석 실습을 해보겠습니다.

Analysis

매체별 광고비가 매출에 미치는 영향 회귀분석 실습

위의 선형회귀분석 알고리즘을 활용한 기능인 하트카운트의 요인분석을 통해 매체별로 어떤 관계를 가지는지 알아보겠습니다.

<레시피>

•요인분석에서, 요인을 분석할 목표 수치형 변수(sales)를 설정하고 [분석]버튼을 누릅니다.

• 변수 하나(단순회귀)와 두개(다중회귀)의 조합으로 회귀분석이 자동으로 실행된 뒤 개별 요인의 설명력을 뜻하는 R2값이 큰 순서대로 정렬됩니다.

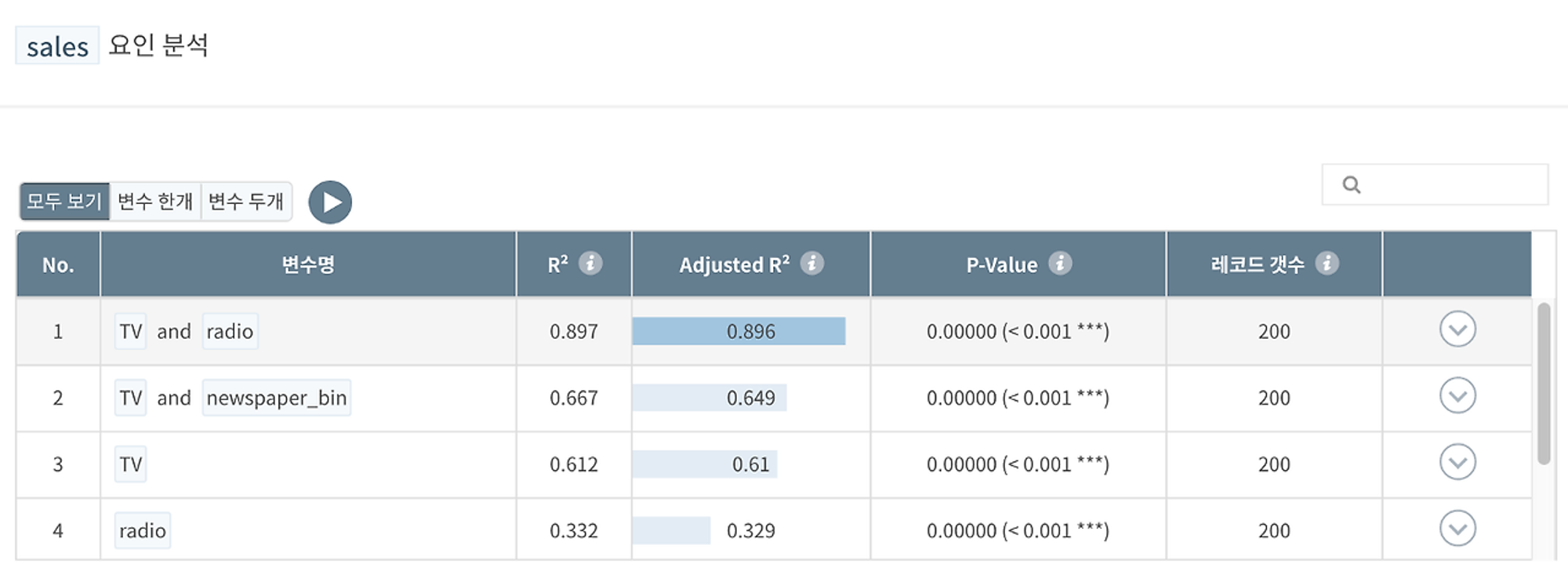
<분석 결과 해석>

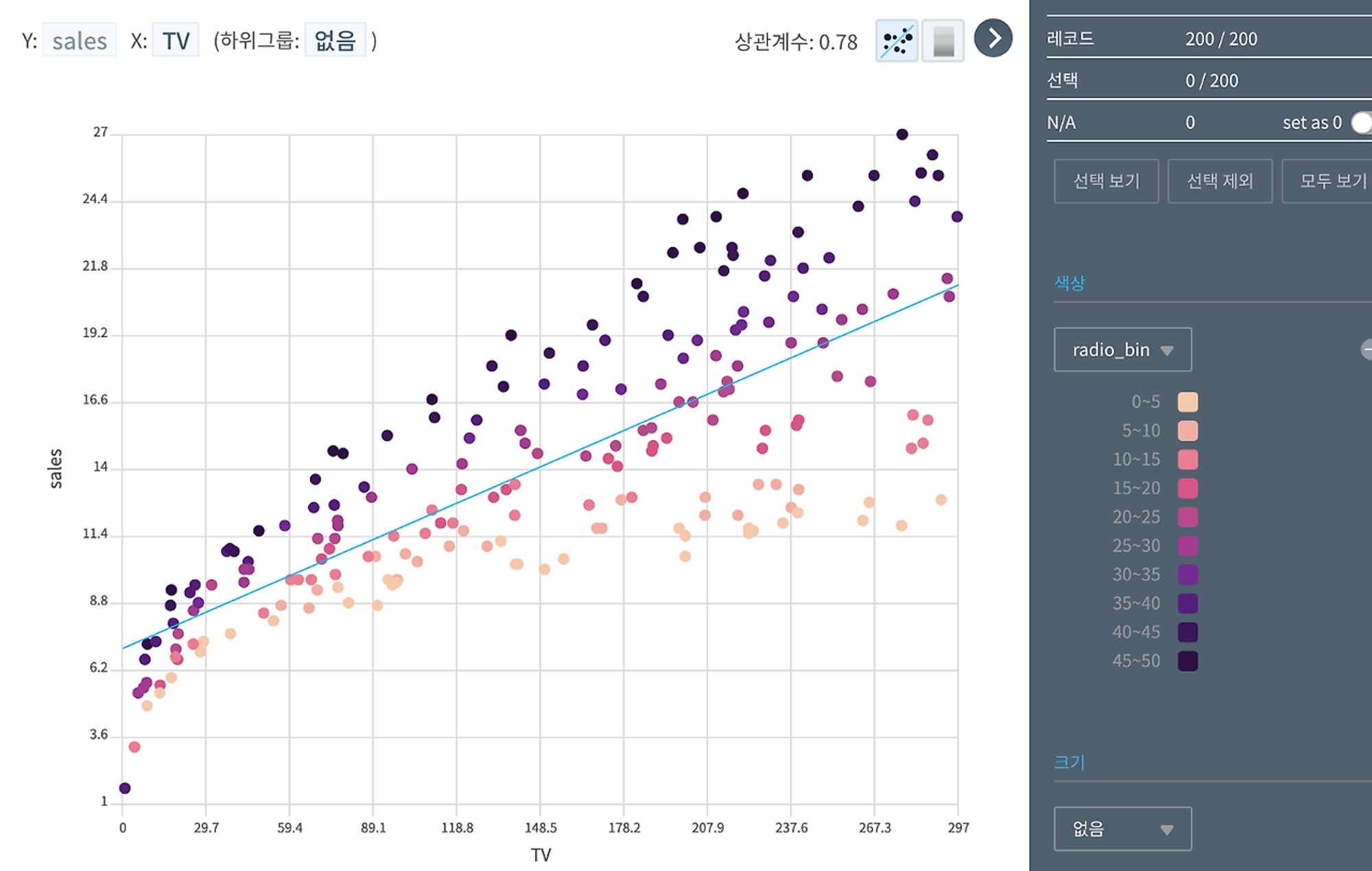
• 다중회귀분석과 단순회귀분석 통틀어 가장 R2값이 높았던 변수를 클릭하면, 해당하는 시각화 그래프를 확인할 수 있습니다.

• TV 광고 지출이 높을수록, 동일(비슷한)한 TV 광고 지출이라면 Radio 지출이 높을수록(색상이 진해질수록) 매출이 상승하는 것을 볼 수 있네요.