Intro: 回帰分析について
今日は変数間の関係を統計的に説明するアルゴリズムである回帰分析について説明します。

線形回帰(Linear Regression)分析
- 変数値(売上、満足度など)の差がどこから来ているのかを知りたいときに使用する最も古く、広く使われている分かりやすいアルゴリズムです。
- 独立変数(X)を持って数値型従属変数(Y)を最もよく説明・予測(Best Fit)する線形関係(Linear Relationship)を見つける方法
- 今後100年後も引き続き使用されるアルゴリズムとして線形回帰分析が第一に挙げられる理由は、モデルの内容を人が直感的に理解できるからです。
線形回帰分析の計算方法 (Least Squares)
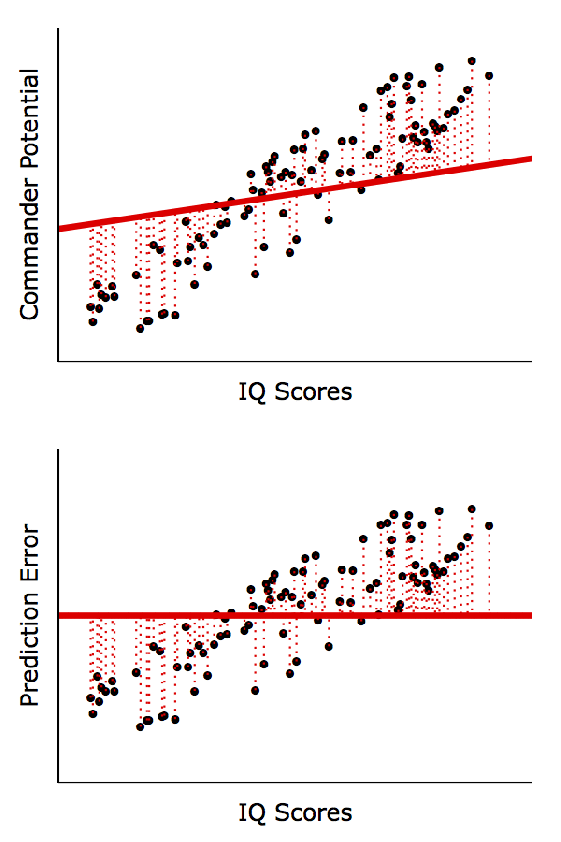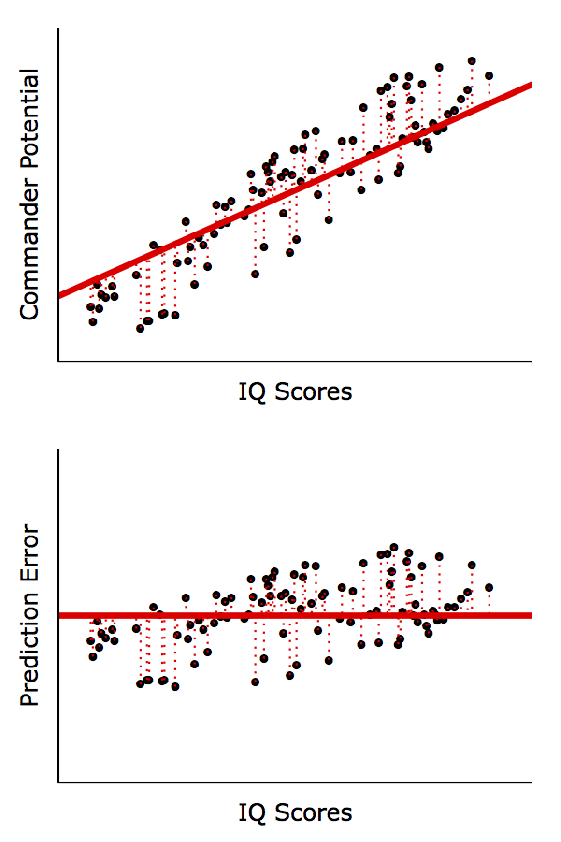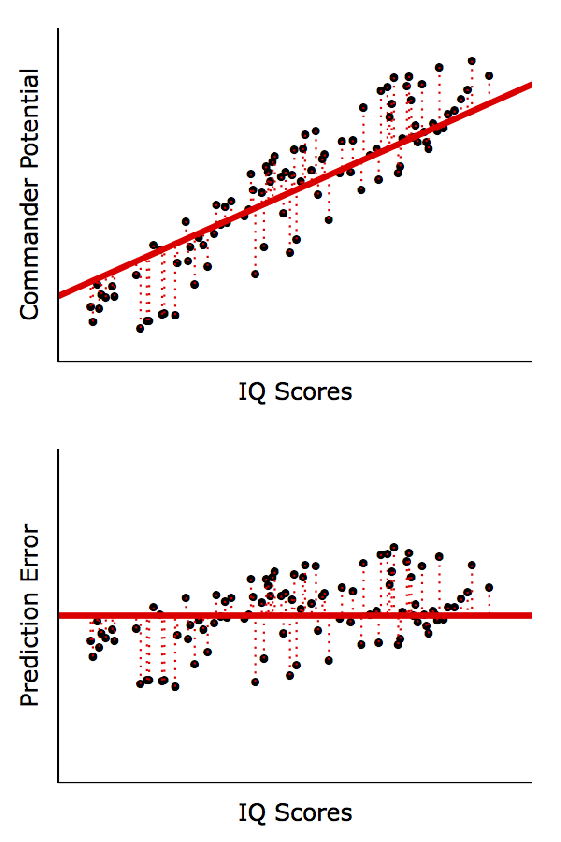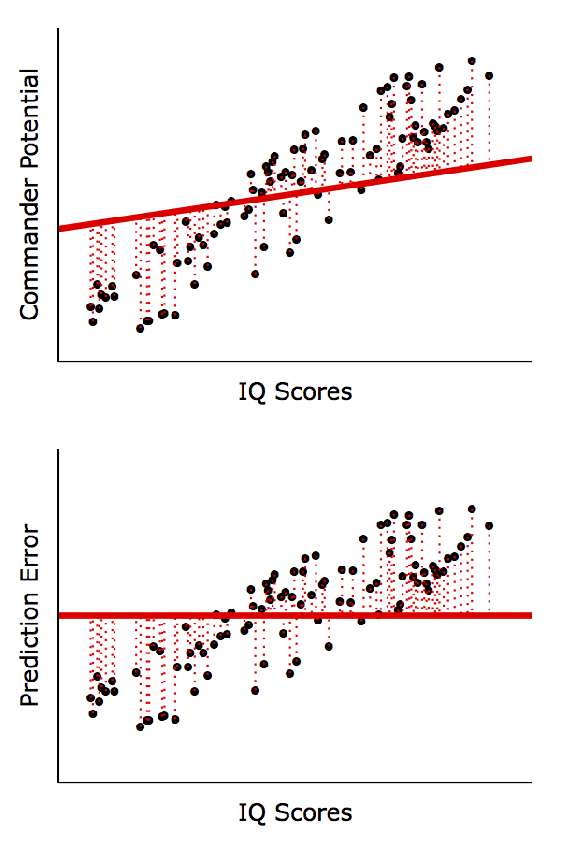
XとYの間に線形関係があると仮定し、実際のY値(点)と予測したY値(直線)の差を最小化する方程式を計算します。
⎮Y = b0 + b1X + error
- b0 : Y軸切片(Intercept); 予測変数が0の時の期待スコアを示す。
- b1 : 傾斜でXが1単位増加したときのYの平均変化値を表す。
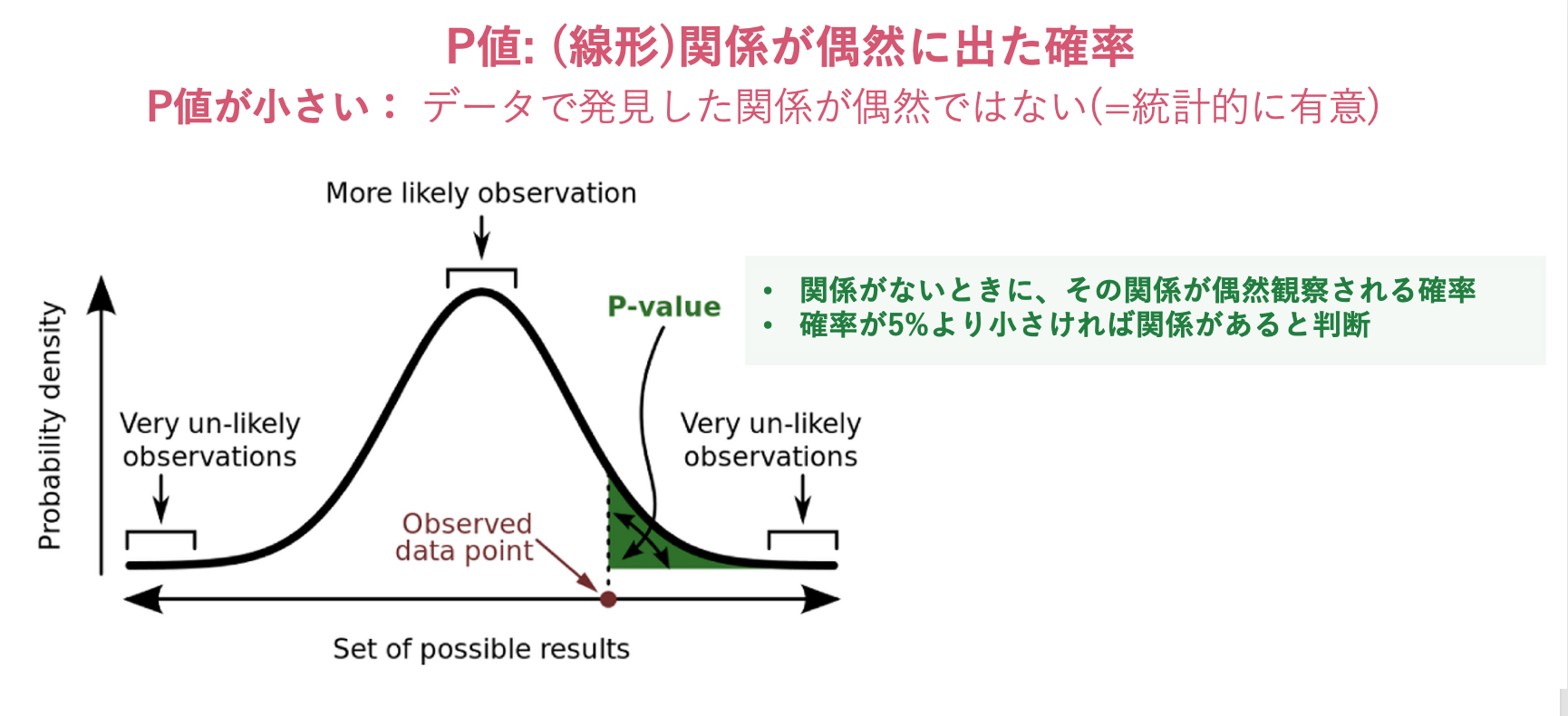
P値(確率値)
- Statistical Significance(統計的有意性)を示す数値で、XとYの間に発見された関係が統計的に有意かどうかを知らせます。
- データを通じて確認した関係が偶然に出た確率で考える。
- P値が0.03であれば、XとYの間に(線形)関係がないにもかかわらず、データサンプリングのミスで関係が偶然発生した確率が3%程度という話です。
- 絶対的な基準はなく、通常0.01~0.05より低ければ有意であると考える。
- 変数間の関係の強さ(Size of an Effect)を示すものではない(P値が0.0001で非常に小さくても、Xの変化によるY値の変化[関係の強さ]は無意味なレベルで微々たる可能性がある)
R2 (R-SQUARED; 決定係数)
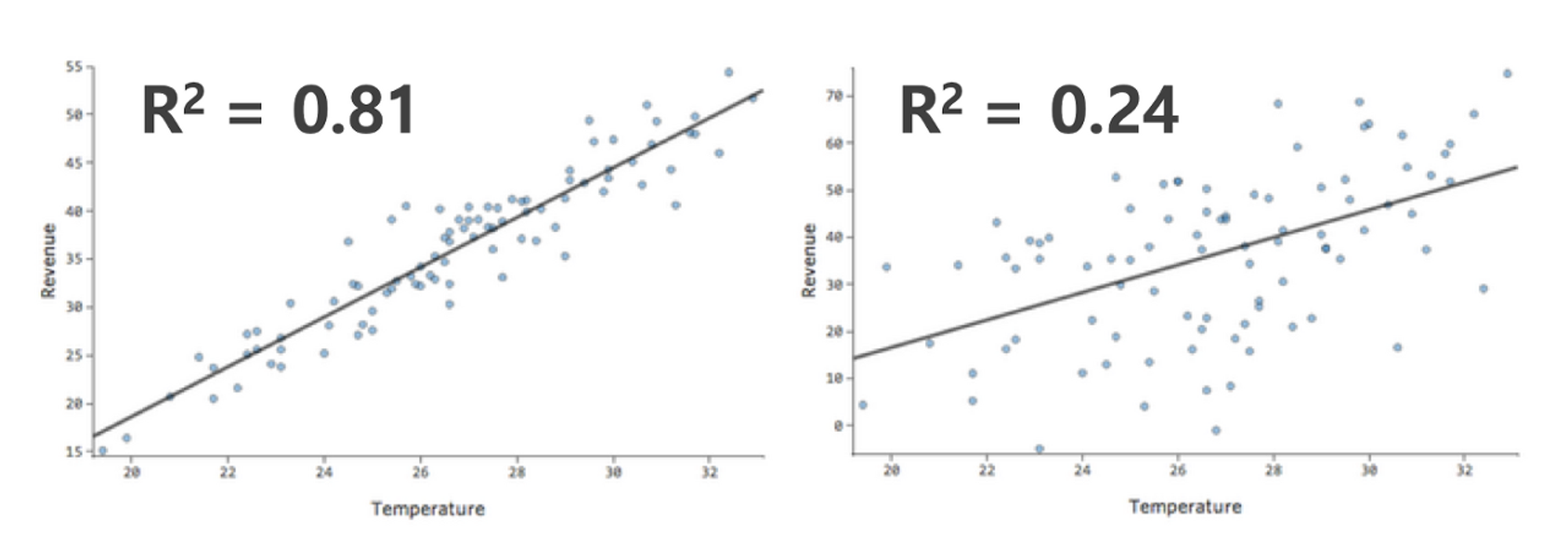
- XがYをどれだけよく説明/予測するかを教えてくれる統計量。
- Goodness of Fit: Xで説明できるY変化量の大きさを表し、0から1の値を持つ(1なら違いを100%説明するという話)
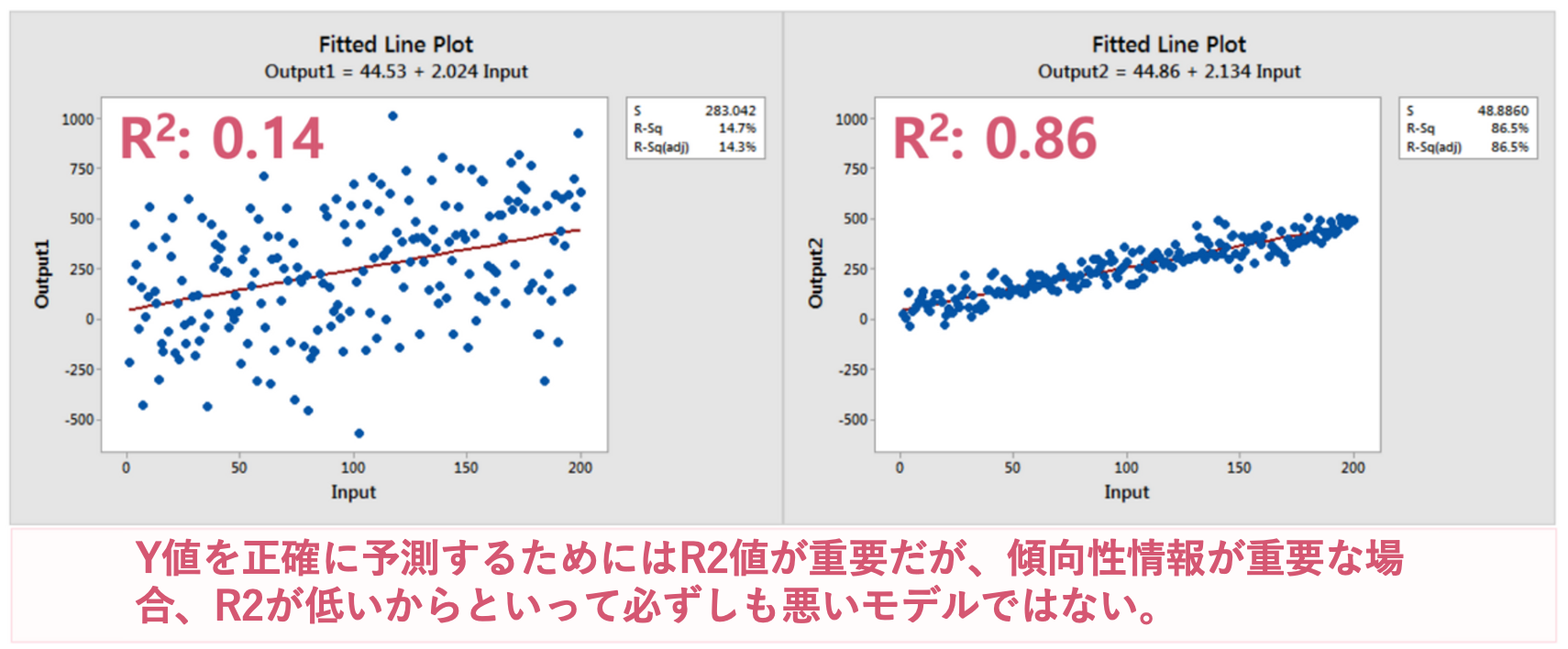
• 下の図のように低い係数が必ずしも悪い(Inherently Bad)わけではありません。
◦ 左、右とも同じ回帰方程式: Y = 44 + 2*X; P < 0.001
◦ 右側のモデルが左側のモデルより予測精度(R2)は非常に高い
(つまり、X値が250であれば、Y値はどの程度になるかをより正確に予測)
◦しかし、変数間の傾向性は同じ: X: 1単位増加 → Y: 2単位増加
(予測の正確さではなく、傾向性を把握することが重要であれば、左、右ともに有意なパターンである)
Analysis in HEARTCOUNT
Dataset
4つの広告媒体と売上が含まれているデータセットで簡単な回帰分析実習をしてみましょう。
📎
Analysis
📍
HEARTCOUNTのユーザーなら、活用例を参考にしてみてください。ビジュアル分析は無料です。統計機能はプレミアム版が必要となります(1ヶ月無料あり) 👉今すぐにトライ
媒体別広告費が売上に与える影響の回帰分析実習
上記の線形回帰分析アルゴリズムを活用した機能であるHEARTCOUNTの要因分析を通じて、媒体別にどのような関係があるかを見てみましょう。
<ステップ>
- 要因分析で、要因を分析する数値型の目的変数(sales)を設定し、[実行]ボタンを押します。
- 変数一つ(単純回帰)と二つ(重回帰)の組み合わせで回帰分析が自動的に実行された後、個々の要因の説明力を意味するR2値が大きい順にソートされます。
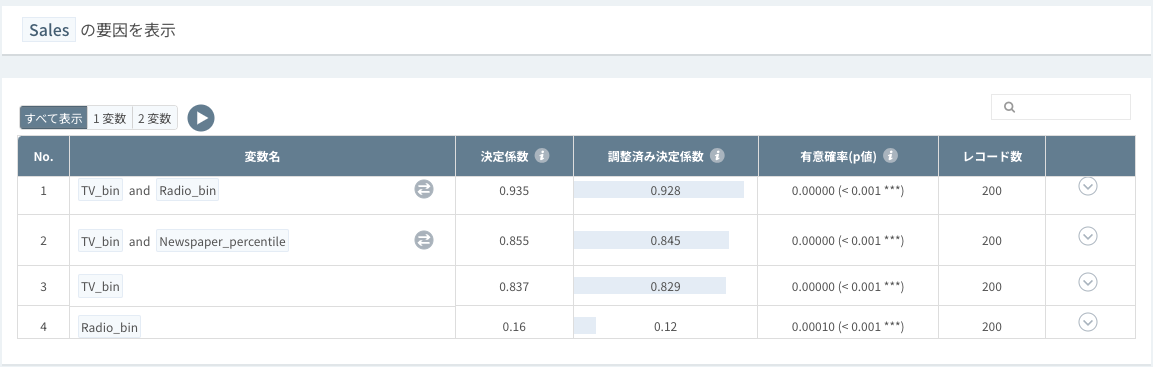
<分析結果の解釈>
- 多重回帰分析と単純回帰分析で最もR2値が高かった変数をクリックすると、該当する可視化グラフを確認することができます。
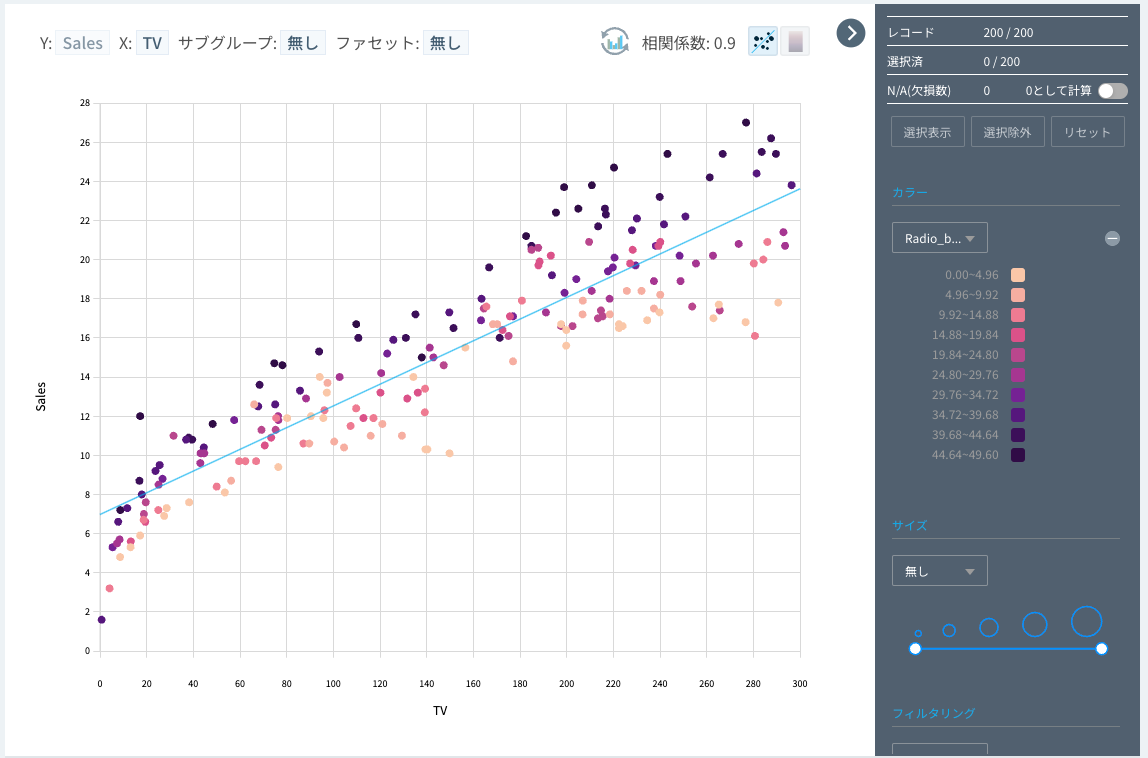
🤍




![[HEARTCOUNT実習例] HR dataset - I(人事分析)](/ja/content/images/size/w540/2024/10/------_--------_-----_--------_-1-.png)