분포 : 개별 레코드 수준의 시각화를 통해 불확실성을 말해야 할 때

집계값(평균)이 아닌, 개별 레코드 수준에서 분석해야 하는 이유

아쉽게도 우리는 개별 레코드 수준의 시각화에 익숙하지 못하다. 바차트, 라인차트 등 데이터를 평균이나 총합으로 요약, 집계하여 보여주는 대시보드 차트에 너무 친숙해진 탓이다.

평균적 이해를 넘어서

평균, 합계 등 집계값으로만 분석/시각화하는 것이 위험한 이유는 이상치(outlier) 등 데이터의 분포 모양과 개별 데이터의 특수성이 묻힐 수 있기 때문이다. 예를 들면, 한두개의 이상치(대부분 값의 범위에서 벗어나 극단적으로 크거나 작은 값)가 전체 평균값을 왜곡할 수도 있고, 이런 이상치는 개별 레코드 수준의 시각화를 통해서만 확인이 가능하다.

불확실성을 직시하기

범주(부서, 상품군, 날짜)를 사용하여 숫자(매출 등)를 집계하지 않고 데이터를 개별 레코드 수준에서 시각화하게 되면, 집계된 추상화된 숫자(평균 매출, 매출 총합)의 확정적인 느낌이 사라지고 필연적으로 불확실성이 드러나게 된다. 데이터 분석을 한다는 것은 이런 불확실성에도 불구하고 어떤 주장을 한다는 것이다.

평균과 합으로 집계된 추상화된 정보에 기대어 의사결정을 내리는 일에서 한 걸음 나아가 데이터에 내재된 불확실성 속에서 실용적 패턴을 찾아 현실에 적용하는 방법을 이해하고 그러한 태도를 익히는 것이 필요하다.

이번 글에서는 개별 레코드를 시각화하는 대표적인 방법인 분포와 산점도(scatter plot)를 살펴 보겠다.

분포 시각화 실습

(1) 범주간의 차이가 의미가 있나요? 비교해보기

우선, HEARTCOUNT 스마트 플롯 메뉴에서 아래 동영상을 참고하며 함께 따라해 보자.

• 평균의 비교: 우측 상단의 바차트 아이콘과 팀구분 옆의 정렬방식 아이콘을 차례로 눌러, 평균 직원만족도가 높은 팀순으로 바차트를 정렬해 보자.
• 박스 플롯(상자그림)을 통한 분포 모양 비교: 팀 내 개별 관측값들의 분포의 모양을 살펴보자. 우측 상단의 박스플롯(왼쪽에서 두번째) 아이콘을 선택하여, 분포(팀 내에서 직원만족도 점수가 퍼진 정도)를 살펴 보자. 개별 팀 내에서 만족도 점수가 더 넓게 혹은 좁게 분포되어 있는지, 중앙값에서 많이 떨어진 이상치(outlier)가 있는지 확인할 수 있다.

• 평균의 신뢰 구간 비교: 이번엔, 팀간 직원만족도의 차이가 유의미한지(우연이 아닌 본질적 차이) 한번 살펴 보자. 아래 동영상에서 확인할 수 있듯이, [하트카운트] -  [스마트 플롯] - [X축에 범주형 변수] - [우측 상단 총 여섯 개의 차트 종류 중 세번째 아이콘 클릭]하면 팀별 평균값의 95% 신뢰구간이 표시된다.

현실의 데이터는 표본이 아니라 전체 데이터인 경우가 많다. 직원 데이터 역시 전체 모집단에서 추출한 샘플이 아니라 전체 직원(=모집단)을 대상으로 하고 있을 가능성이 크다. 이 경우 현실에 존재하지도 않는 가상의 모집단을 상정해서 모집단의 평균을 포함하는 신뢰구간을 따지는 일이 유효하고 타당한 일인지는 생각해볼 필요가 있다고 생각한다. 실무적 관점에서는 해당 집단의 신뢰구간이 상대적으로 더 넓다면, “해당 집단 내 관측값들의 차이가 상대적으로 크고 레코드 수도 적구나.” 정도로 이해하면 좋겠다.

(2) 변수 간 관계를 개별 레코드 수준에서 시각화해보기

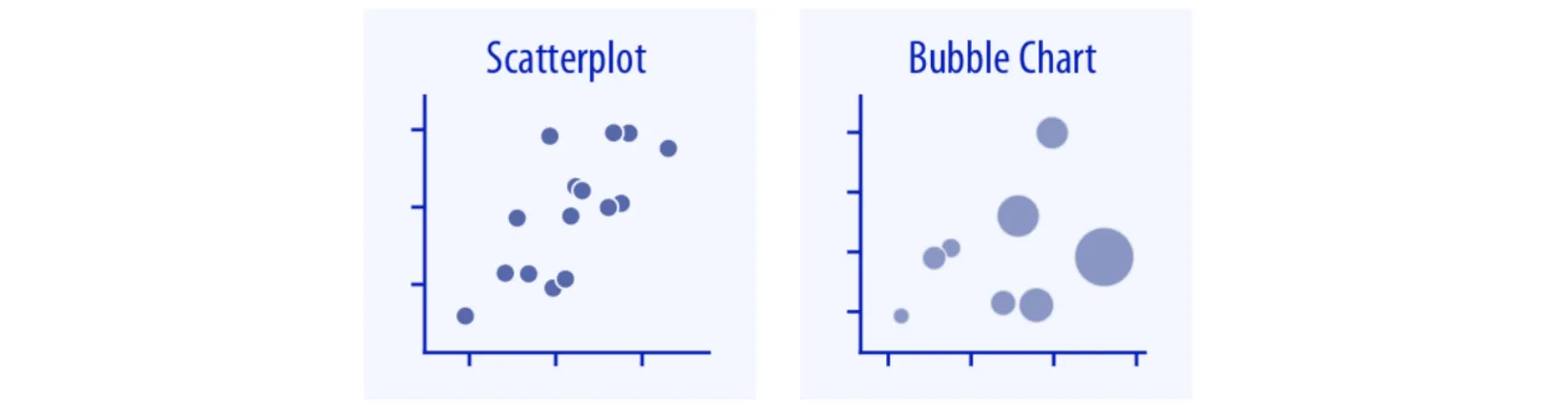
두 개의 숫자 변수 간의 관계(x-y relationships)를 시각화하는 방법에는 산점도(Scatterplot)와 버블차트(Bubble Chart) 두가지가 있다.

산점도가 개별 레코드가 갖는 x, y값을 도형(통상 점)을 사용해 좌표 평면 위에 표시하는 방식이라면, 버블차트는 개별 레코드들을 제삼의 범주형 변수로 묶어서 서로 다른 크기(통상 레코드 개수를 사용)를 갖는 원으로 표현한다.

HEARTCOUNT 스마트 플롯 메뉴에서 동일한 직원(HR) 데이터셋으로 버블차트와 산점도의 차이를 확인해 보자.

버블 차트(Bubble Chart)

Y축에 “직원만족도”, X축에 “매니저소통” 점수를 선택한 후 하위그룹에 “팀구분”을 선택하면 개별 팀이 버블(크기는 각 팀에 속한 레코드 수)로 표현된다.

팀 수준에서 평균적 직원만족도와 매니저소통 점수가 같은 방향으로 움직이는 관계가 있음을 알 수 있다. (개별 레코드가 아니라 하위 그룹으로 집계한 버블차트에서 상관관계라는 용어를 쓰는 건 적절치 않음)

이제, 개별 레코드 수준에서 두 변수(X, Y)의 관계를 살펴 보자.

산점도(Scatterplot)

“하위그룹:없음”으로 바꾸면, 개별 레코드 수준에서 두 변수의 관계를 확인할 수 있는 산점도가 표현된다.

우측 색상 영역의 범례(Legend)에서 특정 팀을 선택하면 해당 팀에 속한 개별 레코드에서 Y와 X 변수간 어느 정도 크기의 상관관계가 있는지 확인할 수 있다. “화면분할:팀구분”하면 각 팀 수준의 상관관계를 개별 창을 통해 확인할 수 있다.

우리가 실무에서 데이터를 시각화하는 이유는 엑셀이나 대시보드의 차트를 통해 익숙한 평균이나 총합이 보여주는 요약되어 확정적인, 그렇지만 미덥지 못한 숫자 뒤의 세계를 들여다 보자는 것이지 더 예쁜 차트를 만드는 것이 아닐 것이다.

평균이나 합으로 요약된 값 뒤에는 다양한 분포를 갖는 개별 레코드들이 있다는 사실을 기억하자. 개별 레코드 수준의 시각화를 통해 평균/합 뒤에 감추어진 불확실성을 두 눈으로 확인하여, 불확실성에도 불구하고 의미있고 실용적인 차이와 관계를 발견하는 것은 취미로 하는 분석과 그렇지 않은 분석을 가르는 주요한 기준이다.

관련 콘텐츠

집계 말고 개별 레코드 수준 분석의 장점

때로는 대시보드만으로는 부족하다 전통적인 대시보드 레벨의 데이터 시각화 및 분석은 시간의 흐름에 따라 각 회사의 상황에 맞추어 미리 정의된 지표들의 추이를 확인하기 위한 목적성을 지니고 있다. 예를 들어 제품별 재고율의 월별 추이, 팀별 평균 판매량 비교 등이다. 추이의 변화를 확인하는 것만으로도 때로는 유의미한 데이터 분석이 될 수 있다. “너희 팀

HEARTCOUNT COMMUNITYheartcount

[Monthly Webinar] 4. 개별 레코드 수준에서의 시각화 기법들 - 상관관계와 분포

집계값이 아닌 개별 레코드(값)으로 시각화하는 방법에 대해 알아 보세요. 또한, ‘평균의 함정’ 등 관련 이론에 대한 설명을 통하여 집계값이 아닌 개별 레코드 수준에서의 시각화가 어떤 면에서 중요한 지 이해하실 수 있어요.

HEARTCOUNT COMMUNITYheartcount