まさに今、AIの大時代が到来しています。ChatGPTをはじめとする超巨大言語モデル(Large Language Model、以下LLM)の登場は、ほぼすべての業界のソフトウェアにLLMが適用される流れを生み出し、もはやLLMが導入されていない製品を探すのが難しいほどです。
特にデータ分析の分野では、LLMがもたらした影響によって市場の様相が大きく変化しています(これについては以前一度ご紹介しました)。平均を出し、合計を計算し、T検定を行い、簡単な可視化をするなど、従来のデータ分析作業は今やChatGPTにデータをアップロードするだけで、自動的にコード作成から計算まで簡単にこなせるようになりました。
このように誰もが数行の指示だけで分析を実行できる時代となり、「データ分析のためにわざわざ統計学のような難しい学問を学ぶ必要があるのか?」という疑問が次第に広まっています。企業の立場から見ても、高価な分析ツールや専門人材を採用する必要はないと判断するケースが増えています。
しかし、ここには大きな誤解があります。多くの人が「統計」を平均や検定を計算する手法としてだけ捉えていますが、統計学の本質は数値を超えて世界を理解するための思考の枠組み、すなわち「統計的思考(Statistical Thinking)」にあるのです。
第1部:統計的思考の本質と役割
統計的思考(Statistical Thinking):世界の不確実性を理解するための枠組み
統計的思考は、以下のように簡単に要約できます。
- 世の中のほとんどの現象は不確実性の下にあるという事実を前提とし(誤差項)
- その不確実性の中でも、体系的な観察と推論を通じて意味のあるパターンや原因を見出せると信じ(パターン認識)
- どんな数値が出たのかということを超えて、なぜその数値が出たのかを絶えず問い続ける思考方法です。
簡単に言えば、統計的思考とは、データの表面だけを読むのではなく、その背後にある文脈や構造を推測しようとする姿勢のことです。たとえば、あるマーケティングキャンペーンの後に売上が増加した場合、単に「売上が伸びた」という結果に満足するのではなく、「本当にこのキャンペーンが原因だったのか?」「他に外部要因はなかったのか?」「同じ結果が他の時期にも再現されるのか?」といった問いを投げかけるのが統計的思考です。これは単にデータアナリストのような専門職だけでなく、Excelレベルでも数字に向き合うあらゆる業界のすべての人にとっての課題でしょう。
もう少し詳しく見てみましょう。統計学者たちはこの複雑な世界の構造を説明するために、驚くほどシンプルでありながら強力な一つの数式を提案しました。中学校の数学レベルの関数の概念さえ理解していれば分かるこの数式は、統計的思考の核心を凝縮した象徴とも言えます。
Y = f(X) + e : 世界の現象はパターンと不確実性で成り立っている
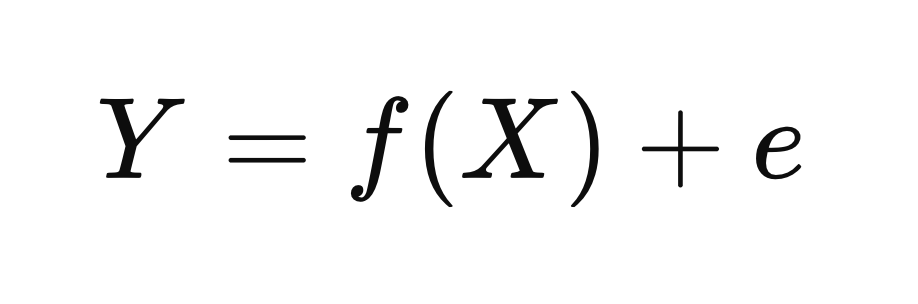
この数式はシンプルでありながら、私たちが現実を見る思考の枠組みそのものを変えてしまいます。
- Yは、私たちが積極的に知りたい「結果」あるいは「現象」です。
たとえば、顧客離脱率、売上、製品のクリック率、治療効果などがこれにあたります。 - Xは、そのような結果に影響を与える要因や条件です。
顧客の年齢、価格、接触経路、服用している薬、実験群かどうかなど、さまざまな説明変数がここに含まれます。 - f(X)は、XがYに与える構造的かつ体系的な影響です。
言い換えると、世界の仕組みや動作原理を表す関数です。 - eは、私たちが説明できない誤差項です。
つまり、不確実性や例外の領域を意味します。
この数式を少しだけ考えてみるだけで、次のような事実が分かります。私たちがYという結果を、自分たちが望む方向へと変えたい場合――たとえば、売上を上げたいとか、社員のパフォーマンスを改善したいとき――f(X)を改善すれば「誤差e」を減らすことができるということです。売上(Y)が100で、f(X)で説明できる部分が80%なら、誤差は20%になります。このとき、f(X)で説明できる部分を99%まで高めることができれば、誤差は1%に減るのです。
この数式を少しだけ捻って考えてみると、次のような事実が分かります。私たちがYというものを望ましい方向に変えたいと思うとき、たとえば売上を上げたい、社員のパフォーマンスを改善したいという場合には、f(X) を改善することで e(誤差) を減らせるということです。
売上(Y)が100で、f(X)で説明できる部分が80%であれば、誤差は20%になります。このとき、f(X)で説明できる部分を99%にまで高めることができれば、誤差は1%にまで減るでしょう。
もう少し分かりやすく、具体例を挙げてみましょう。たとえば、顧客満足度(Y)を高めたいと仮定してみてください。顧客満足度自体は主観的で定量的に測るのが難しいYですが、応対時間、問い合わせ処理の正確さ、配送スピード、価格の妥当性といったものは、Xとして私たちが測定・調整可能な要素です。これらのXをしっかり定義し、それらがどのように作用しているかを把握した精緻なf(X)を構築できれば、「顧客満足度」という結果をより安定的に説明・予測・改善することができるようになります。
たとえば、問い合わせ処理の正確さが顧客満足度に与える影響を理解していて、現在の処理精度が低いとすれば、それをどれだけ改善すれば顧客満足度がどの程度向上するかを見積もることで、適切な戦略を立てることができるでしょう。
因果推論の必要性と相関関係に対する誤解
しかしここで、重要な問いが生まれます。
「果たしてXとYの間には本当に因果関係があるのだろうか?」
データを分析していると、互いに密接に動く変数(相関関係のある変数)をよく見つけます。たとえば、広告費が増えた時期に売上も上がったとしましょう。この2つの変数の間に統計的に有意な相関関係があったとしても、「広告費を増やせば売上が上がる」とすぐに主張できるでしょうか?もしかすると、広告費と売上の両方が、季節的な要因やプロモーション、競合状況といった第三の要因によって同時に影響を受けた可能性はないでしょうか?
このように、XとYが一緒に動いている(correlation)という事実だけでは、XがYの原因である(causation)とは断定できません。そしてこれこそが、多くのデータに基づく意思決定で繰り返し発生する致命的な誤りなのです。
ここで登場するのが「因果推論(causal inference)」です。因果推論は、観察されたデータの中から単にパターンを見つけるのではなく、「ある原因を変えると結果も変わるのか?」という問いに科学的にアプローチする方法です。つまり、私たちがすべてのデータ分析を通じて本当に知りたいのは、「何が起こったのか?」ではなく、「何を変えれば、より良い結果が得られるのか?」なのです。
このために、因果推論は次のような重要な考え方を含んでいます:
- 介入(intervention):あるXを変えると、Yはどのように変わるだろうか?
- 反事実的思考(counterfactual):もし別の選択をしていたら、結果はどうなっていただろうか?
- 交絡変数(confounder):XとYの因果関係を歪める第三の要因は何か?
- 代理変数(proxy variable):直接観察できない要因を、どの観察可能な変数で代替できるか?
これらの問いは、単純な統計モデルやLLMベースの平均/集約的な視点からの分析だけでは解決が困難です。なぜなら、多くのAIモデルは「既存のデータに存在するパターンを繰り返し学習する」ことに重点を置いているからです。
しかし、因果推論は「存在しなかった状況」、つまり「起こらなかった出来事」に対して想像力と論理的仮定を通じた検証が必要となります。こうした思考は本質的に人間中心の思考であり、データを超えた判断力が求められます。
例を挙げましょう。先ほどの Y = f(X) + e の例に戻って、ある会社が顧客離脱率(Y)を下げるために様々な施策を講じているとします。コールセンターの対応スピード、割引クーポンの提供有無、メンバーシップランクの制度などをXとして設定し、それらが離脱率にどのような影響を与えるかを分析しようとしています。
ここで単純に「メンバーシップランクの高い顧客は離脱率が低い」という相関を見つけたとしても、「メンバーシップランクを上げれば離脱率が下がる」とは言えません。
実際には「満足度が高い顧客ほどメンバーランクも高く、離脱もしにくい」可能性があるからです。
この場合、顧客満足度という隠れた交絡変数(confounder)を考慮しなければ、誤った結論にたどり着くことになります。
交絡変数の統制方法:RCT、PSM、DiD
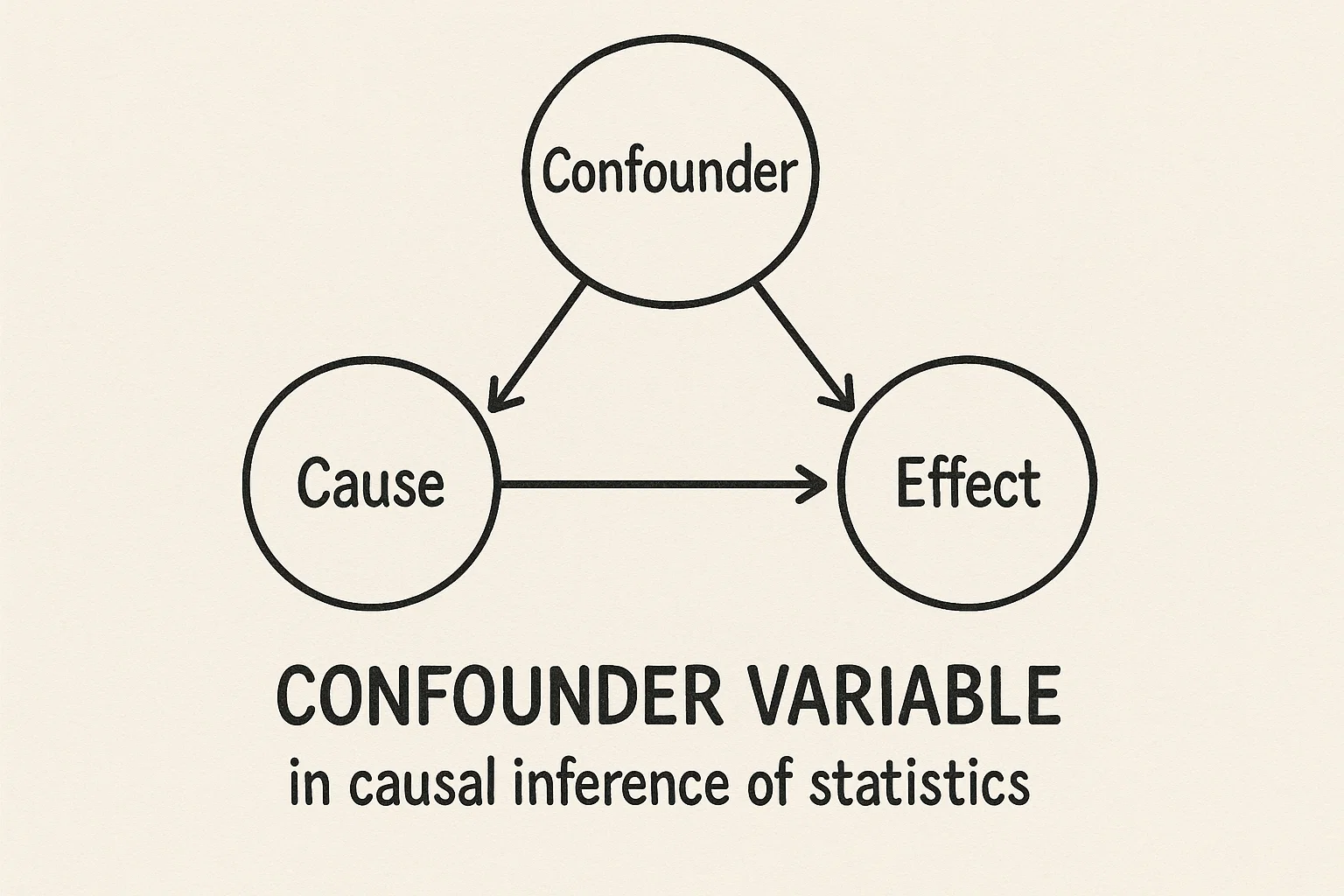
では、このような場合にはどうすればよいのでしょうか?
「顧客満足度」という交絡変数(confounder)をコントロールするために、私たちが使える方法はいくつもあります。
統計学者たちは、このような状況を解決するために、長い年月をかけてさまざまなフレームワークを開発してきました。
- 無作為実験(ランダム化比較試験、Randomized Controlled Trial:RCT)
最も理想的な方法は、無作為実験(RCT)を設計し、顧客をランダムに分けて、一方のグループにのみメンバーシップランクを引き上げる方法です。
このようにすれば、満足度を含むすべての外部要因が両グループ間で平均的に等しくなるため、メンバーシップランクの変化が離脱率に与える因果効果を比較的正確に把握することができます。
- 傾向スコアマッチング(Propensity Score Matching:PSM)
しかし、実際のビジネス環境ではこのような実験(RCT)が常に可能とは限らないため、観察データに基づいて因果推論を行わなければならない場合が多くあります。
その際に使える代表的な手法の一つが、**傾向スコアマッチング(Propensity Score Matching:PSM)**です。
PSMでは、メンバーシップランクが高い顧客とそうでない顧客を、「顧客満足度」や「顧客ロイヤルティ」などの主要な変数に基づいて、似た条件のペア同士でマッチさせ、その2つのグループ間で離脱率を比較します。
このようにすることで、メンバーシップランク以外の条件が似通った集団間での比較が可能になり、メンバーシップランクそのものの効果をより分離して分析することができます。
- 차분의 차분(Difference-in-Differences, DiD)
もう一つの方法として挙げられるのが、差分の差分(Difference-in-Differences:DiD)手法です。
この方法は、政策変更の前後における変化を基準として、メンバーシップ特典が強化されたグループとされていないグループの離脱率の変化幅の差を比較します。
単なる時系列比較よりもはるかに妥当性のある根拠を提供し、政策導入前後の外部環境の変化もある程度コントロールすることが可能です。
このように、観察データから因果関係を見出すためには、いかにして交絡要因(ノイズ)を統制するかを体系的に検討するプロセスが不可欠であり、これは単なる相関分析や、LLMによる統計出力では代替できない統計的思考の核心領域であると言えるでしょう。
LLM時代においても依然として重要な統計的思考の本質
私たちは今、統計的思考の上にさらに一段階進んだ地点に立っています。
データを読み解く「統計的思考」に加え、**世界を変えるための介入の論理(因果的思考)**を手に入れたのです。
これは、AIと自動化があふれる時代において特に重要です。
なぜなら、AIがどれほど精密になったとしても、
「どんなデータをどう収集すべきか?」
「この変数と結果の間に因果的なつながりはあるのか?」
「モデルの出力をそのまま信じてもよいのか?」
といった根本的な問いに答えるには、まさにここまで紹介してきた統計的思考が必要だからです。
実際、私たちは日常の中ですでにこうした問いを自然に投げかけているのです。
「なぜあの人は退職したのだろう?」
「どうすればパフォーマンスを向上させられるだろう?」
「何が顧客を満足させるのだろう?」
「このアクションを取ったら、本当に指標は改善するのだろうか?」
しかし、前述の数式にもあったように、統計とは単なる数値の計算ではなく、この世界の「原因」と「結果」を構造的に理解し、予測し、そして変化させるための思考の枠組みです。
そして、私たちが日常で直面する数えきれない「なぜ?」や「どうすれば?」という問いに答えるために、この思考法は今この瞬間も、最も強力な道具として機能し続けています。
これこそが、統計的思考がLLMの時代においても人間が必ず持つべき、最も重要な「思考の武器」である理由なのです。
第2部:LLMの原理と限界 ― 人間の思考を代替できるのか?
では、再びLLMに話を戻しましょう。
LLMは、膨大な過去データをもとに、次に来る単語や文を最も適切に、確率的に予測する仕組みで動いています(これを難しい言葉で「条件付き確率推定(conditional probability estimation)」と言います。ここで「確率」という言葉をぜひ覚えておいてください)。
つまり、与えられた単語の並び(シーケンス)から、次に出現する単語の確率を計算し、最も確率が高い出力を生成するという方法です。
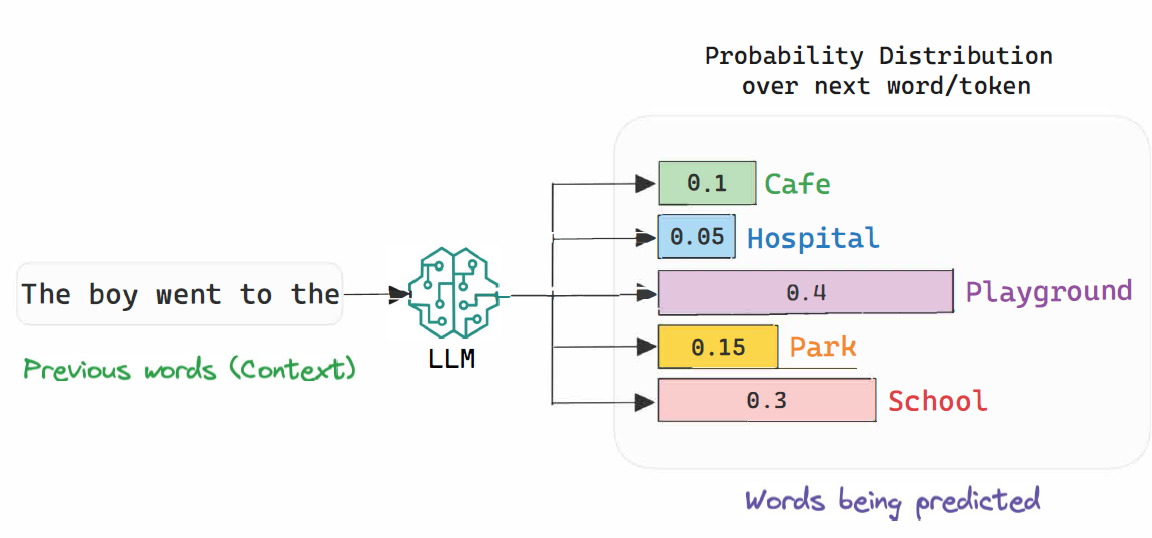
しかし、LLMのこうした特性のために、一部ではLLMを「確率論的オウム(Stochastic Parrot)」と呼び、批判する意見もあります。
現代を代表する言語学者ノーム・チョムスキー(Noam Chomsky-san)をはじめとする一部の学者たちは、LLMは膨大なテキストを単に統計的に模倣・組み合わせているだけの機械であり、人間のような本当の意味での「理解(understanding)」は不可能であると指摘しています。
Chomsky-sanの見解によれば、言語とは単なるデータの蓄積やパターンの繰り返しではなく、人間に内在する認知的な構造が働いてこそ生まれる、創造的かつ革新的な行為であるとされています。

このような批判を説明する際によく使われる比喩が、**無限のサル定理(Infinite Monkey Theorem)**です。
これは、「無数のサルが無作為にタイプライターを打ち続ければ、最終的にはシェイクスピアの戯曲のような傑作が偶然完成する可能性が限りなく100%に近づく」と数学的に示された概念です。
しかし、そうして完成された文章を見て、「サルがシェイクスピアを“理解”した」と言えるでしょうか?
サルは単に無作為なパターンを永遠に繰り返したにすぎません。
Chomsky-sanをはじめとする批判者たちは、LLMの言語能力も原理的にはこの“無限のサル”と大差ないと主張します(もちろん、サルは完全にランダムに打っているのに対して、LLMは条件付き確率分布に基づいているという違いはありますが)。
ジェフリー・ヒントン-sanの反論:人間とLLMの思考の類似性
しかし最近、このような批判に正面から反論している代表的な人物がいます。
それが、ディープラーニングの第一人者である**ジェフリー・ヒントン(Geoffrey Hinton-san)**です。
Hinton-sanは、LLMが「確率論的オウム」にすぎないという主張に対して強く反対しています。
彼は、人間も本質的にはLLMと大きく変わらない仕組み――すなわち、ニューロンのネットワークを通じてデータを蓄積・学習し、世界を理解しているのだと強調します。
つまり、人間の言語や思考能力も、大量のデータを基に統計的に学習された結果であり、そうした観点から見れば、人間の思考とLLMの動作原理には根本的な違いはないというのです。
たとえば**ハルシネーション(幻覚)**のような現象も、人間の記憶が歪んだり誤認したりするのと本質的に大きな違いはない、という考え方です。
LLMは統計的・因果推論的な思考を行う能力を持っているのか?
このように、超巨大言語モデル(LLM)は、私たちが入力したテキストをもとにもっともらしい文章を生成することができますが、その出力が本当に「人間のような思考(thinking)」や「理解(understanding)」を伴っているのかどうかについては、依然として多くの議論の余地があります。
Chomsky-sanが正しいのか、Geoffrey Hinton-sanが正しいのか――それは私のような一般人が判断すべき領域ではないかもしれません。
しかし少なくとも、次の2点は重要な観点として押さえておくべきでしょう。
- LLMは、学習したデータに基づく“ある種の体系(system)”に閉じ込められている可能性があること
- この前提のもとで、LLMを活用したデータ駆動型の意思決定には可能性と限界の両面があるということ
前述したように、特に因果推論的思考(causal reasoning)や反事実的推論(counterfactual reasoning)のような高次の認知能力は、人間の思考の核心であり、統計的思考の最も重要な要素です。
果たしてLLMがこの領域をどこまで支援できるのか、あるいは一部でも代替できるのか――それを考える手がかりとして、次に紹介する2つの論文を一緒に見てみましょう。
『Reasoning or Reciting?』:学習されたパターンの再現、それ以上ではないのか?

この論文は昨年、ACL Anthologyに掲載されました。
LLMが単に学習済みのパターンを再構成するだけでなく、**真の意味で一般化された推論(generalized reasoning)**ができるのかを評価するために、**反事実的課題(counterfactual task)**を設計して実験が行われました。
主な課題は以下の通りです:
- 進数変換を伴う算術課題:
十進法(base-10)の代わりに九進法(base-9)など、LLMが慣れていない方式で数値演算を行わせる課題 - 空間的推論タスク:
既存の座標系を回転・反転させたうえで、方向を正しく推論できるかを確認 - プログラミング課題:
通常の「0から始まるインデックス」ではなく、「1から始まるインデックス」を用いる仮想のプログラミング言語環境におけるコード推論
これらのタスクは、単なる記憶や暗記の再現では対処しにくい設計になっており、LLMの汎化・推論能力の限界を測定する目的で行われました。
このように、既存の学習データとは異なる新しい規則や構造を適用したさまざまな反事実的(counterfactual)条件を導入した結果、GPT-4を含む最新のLLMは、従来の条件下に比べて著しくパフォーマンスが低下しました。
注目すべきなのは、モデルが「条件そのものを理解できなかった」わけではないという点です。むしろ、多くのケースでモデルは提示された前提条件を言語的に理解しているように見えたにもかかわらず、その条件に基づいて正しく課題を遂行する能力が不足していたということが明らかになりました。.
『Theory Is All You Need』:"理論"を欠いたAIの根本的限界

この論文は、より根本的な次元でLLMの限界について考察しています。
まず、人間がどのように思考するかを振り返るところから始まります:
- 人間は経験をもとに「理論」を構築し、
- その理論を使って未知の状況に対する仮説を立て、
- その結果を予測する能力を持っています。
論文では、こうした人間の創造性の核心には「データと信念の非対称性(data-belief asymmetry)」があると述べられています。
つまり、人間は既存のデータと一致しなくても、自らの理論や信念を基に新たな可能性を信じて追求できるということです。
その象徴的な例として、著者らはライト兄弟による飛行機の発明を挙げています。
一方、LLMはこのような理論的な冒険や信念に基づく創造性を持っておらず、あくまでも過去のデータに存在したパターンに依存しています。
つまり、LLMは本質的に過去志向であるというわけです。
これはすなわち、LLMには創造的な反事実的思考(counterfactual reasoning)や、理論に基づいた積極的な因果推論を行うことが難しいという根本的な限界があることを意味します。
…ここで私たちが語っている「信念」とは、既存の証拠を超えたり、無視したり、超越したりできる信念のことです。
新しいアイデアや知識の創出には、未来を見据えた、かつ既存の観点に反する(contrarian)視点が不可欠です。しかし、AIベースの計算・認知システムは本質的に統計的かつ過去志向であり(すなわち、過去データの相関、関連性、平均値などに依存する)、
データと信念の間に暗黙の「対称性(symmetry)」を前提としているため、
既存の常識を打ち破るような反対的で未来志向の推論や思考を行うことが困難なのです。
— Felin, Teppo & Holweg, Matthias. (2024). Theory Is All You Need: AI, Human Cognition, and Causal Reasoning.
第3部:LLMと統計的思考のシナジー ― より良い意思決定のための可能性
ここまで、LLMが本質的に持つ限界について議論してきました。
特に、因果推論のような高度な統計的思考において、LLMは理論的・構造的な制約を抱えていることが明らかになりました。
しかしそれにもかかわらず、実務の現場ではここ数年、研究者や企業がLLMを補助的なツールとして活用し、統計的思考の精度を高め、業務の効率を最大化するさまざまな事例を報告しています。
因果構造発見の効率性向上(LLM支援型因果発見:LLM-Augmented Causal Discovery)
2024年に発表された研究では、GPT-4を活用した新しい因果構造学習手法が提案されました(Using GPT-4 to guide causal machine learning)。
この研究では、実際のデータを一切与えず、変数名のみをGPT-4に提供し、それらの変数間にどのような因果関係があるかを推論させ、**因果グラフ(causal graph)**を作成するよう指示しました。
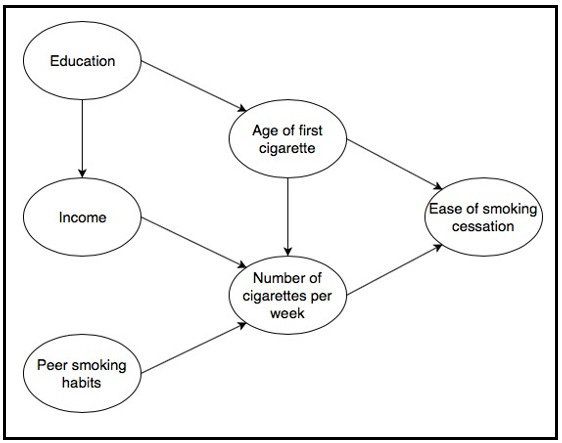
結果は非常に驚くべきものでした。評価によると、GPT-4が生成した因果グラフは、純粋なデータ駆動型のアルゴリズムよりも高い精度を示し、さらにはドメイン専門家が作成した因果構造とほぼ同等の正確さを持っていたのです。
さらに重要なのは、GPT-4の提案を既存の統計的因果学習アルゴリズムと組み合わせたとき、ドメイン専門家レベルに非常に近いハイブリッドモデルが得られたという点です。
これはビジネスの現場において非常に大きな意味を持ちます。
これまでは、たとえばサプライチェーンの崩壊や顧客離脱の原因を特定するために、多くのドメイン専門家によるブレインストーミングが必要でした。
しかし今では、LLMを活用することで、ドメイン知識や常識を手軽に補完し、自動化された形で因果構造を仮定・検証できるようになり、実務担当者の統計的思考を強力にサポートできるのです。
マーケティングにおける反事実的思考(Counterfactual Reasoning)のシミュレーション
2023年、スタンフォードの研究チームは、GPTモデルがテキストベースのさまざまなマーケティングシナリオにおいて、因果関係の推定(97%)および因果効果の予測(92%)で高い精度を示したと報告しました(リンク)。
これにより企業は、次のような反事実的(counterfactual)な問いをLLMに投げかけ、それを意思決定に活用し始めています:
- 「もしこの広告キャンペーンを冬ではなく夏に実施していたら、成果はどう違っていただろうか?」
- 「このキャンペーンをメールではなくソーシャルメディアで行っていたら?」
これを踏まえ、LLMは既存のマーケティングデータをもとに、もっともらしい(plausibility の高い)結果を提示し、
実際には高コストの実験を行う前に、戦略的選択肢の優先順位を意思決定者が明確にできるよう支援しているのです。
意思決定支援と説明可能な(Explainable)因果推論
近年では、因果推論の結果を企業内部の非専門家にも理解しやすい形で翻訳する手段として、LLMが活用されるケースが増えています。
LLMは、複雑な統計的推論のプロセスや結果を自然言語でわかりやすく説明することで、データアナリストと意思決定者の間のコミュニケーションを円滑にする役割を果たしています
(Large Language Models for Causal Discovery: Current Landscape and Future Directions)。
金融分野では、Fin-Forceというプロジェクトにおいて、経済ニュースや政策発表などの多様なインプットをもとに、LLMが妥当性(plausibility)のある反事実的な未来シナリオを生成し、
政策変更による潜在的影響を意思決定者が手軽に評価できるよう支援しています。
最終的にすべてのデータ分析の目的は「より良い意思決定」にあるという点を踏まえると、
このようなLLMの活用は、今後さらに注目すべき展開だと言えるでしょう
(Deriving Strategic Market Insights with Large Language Models: A Benchmark for Forward Counterfactual Generation)。
近年では、因果推論の結果を企業内部の非専門家にも理解しやすい形で翻訳する手段として、LLMが活用されるケースが増えています。
LLMは、複雑な統計的推論のプロセスや結果を自然言語でわかりやすく説明することで、データアナリストと意思決定者の間のコミュニケーションを円滑にする役割を果たしています
(Large Language Models for Causal Discovery: Current Landscape and Future Directions)。金融分野では、Fin-Forceというプロジェクトにおいて、経済ニュースや政策発表などの多様なインプットをもとに、LLMが妥当性(plausibility)のある反事実的な未来シナリオを生成し、
政策変更による潜在的影響を意思決定者が手軽に評価できるよう支援しています。最終的にすべてのデータ分析の目的は「より良い意思決定」にあるという点を踏まえると、
このようなLLMの活用は、今後さらに注目すべき展開だと言えるでしょう
(Deriving Strategic Market Insights with Large Language Models: A Benchmark for Forward Counterfactual Generation)
LLM時代における、統計的思考とAIのシナジーが導くより良い意思決定
ここまで、LLM(超巨大言語モデル)の時代において、伝統的な統計や因果的思考が果たして今も意味を持つのか、またLLMがその中でどのような役割を果たせるのかについて、さまざまな観点から考察してきました。
多くの人がLLMの登場とともに、伝統的な統計を単なる「平均や合計を計算する古い手法」と見なす傾向がありますが、それは統計学の本質に対する誤解に他なりません。
統計は決して旧世代の遺物ではなく、数字を扱う技術にとどまらず、不確実性のある世界を理解し、説明し、予測し、それに基づいてより良い意思決定を行うための強力な思考の枠組みなのです。
私たちが本当に知りたいのは「どんな数字が出たのか?」ではなく、「なぜその数字になったのか?どうすれば望ましい方向に変えられるのか?」なのです。
つまり、すべてのデータ分析の核心には意思決定があり、その意思決定を支えるために不可欠なのが、統計的思考(statistical thinking)なのです。
このような文脈において、今後のデータ分析の進むべき方向は明確です。
それは、人間の統計的思考能力とLLMの言語処理能力が相互補完的に融合することです。
LLMが人間の思考や分析を「置き換える」のではなく、統計的思考のプロセスをより明確にし、意思決定の選択肢を豊かにし、より良い判断を導くための支援ツールとして活用されるとき、データ分析はその真価を発揮するでしょう。
なぜなら、私たちが目指すべきデータ分析の最終的な目的は、「人間がデータを通じて世界を深く理解し、より良い意思決定を下すこと」だからです。
こうした人間とAIの協働が成功すれば、企業や組織はこれまでにないほど賢く、戦略的な判断ができるようになると期待されます。
HEARTCOUNTもこのような問題意識をもとに、ユーザーの質問に込められた意図を統計的思考の観点から解釈し、AIが現場で実用的なインサイトを自動で提示する仕組みを目指しています。
LLMは分析を完全に置き換えるのではなく、より深い思考を可能にし、そしてその思考がより良い意思決定を導く未来を、HEARTCOUNTは描き、そして今この瞬間も設計しています。
これこそが、LLM時代におけるデータ分析の真の進むべき方向性であると提案し、この文章の締めくくりとします。
→ LLM + Statistical thinking = Better decision making