EDA (探索分析) について

EDAの実習に使用するデータセットの説明

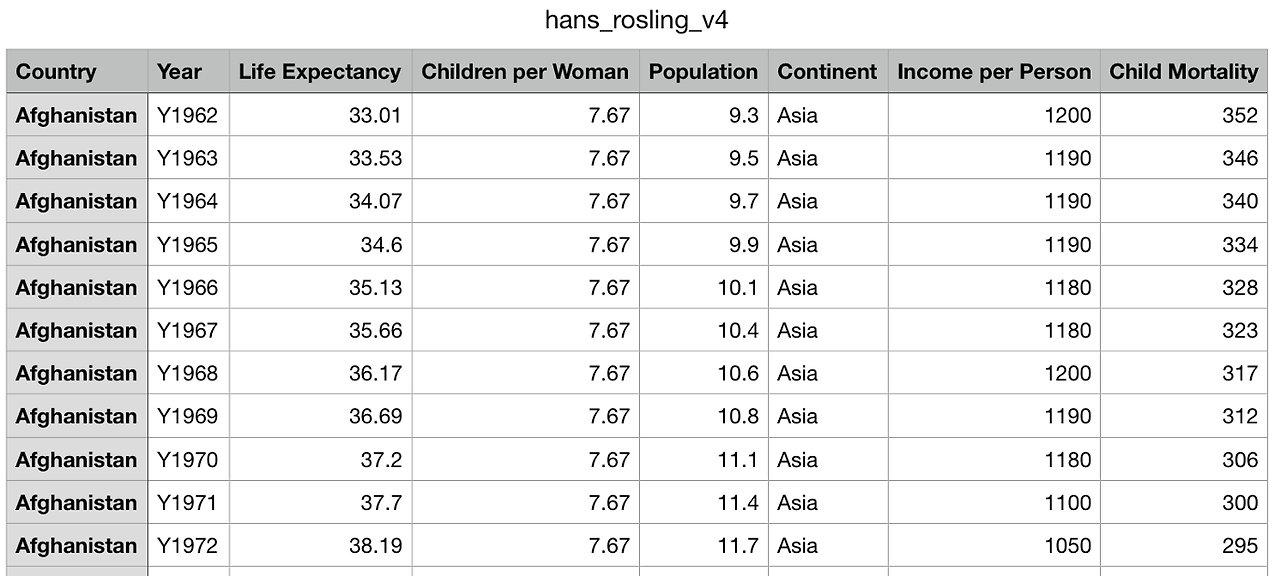
このブログで使用するデータは、Hans Rosling がデータの視覚化を通じて人々が基本的な事実関係についてどれだけ無知であるかを明らかにするために使用したデータセットで、以下の変数から構成されています。

• Country: 国名
• Year: 平均寿命などの各種の統計値が集計された年
• Life Expectancy: 平均寿命
• Children per Woman: 女性1人あたりの出生数
• Population: 人口
• Continent: 国が属する大陸名
• Income per Person: 1人あたりの所得(単位$)
• Child Mortality: 5歳以下の乳幼児1,000人あたりの死亡者数

Descriptive Analytics (記述分析):

記述分析は、データを事実として記述(describe)することであると定義することができます。(テーブル形式で整理された)データさえあれば、記述分析によって「What Happened?」に関する質問に回答することができます。

件数を集計したり(例: 何人が訪問したのか?)、平均を比較したり(例: 過去四半期の商品カテゴリー別の売上はどのくらいだったのか?)など、データを要約してデータに含まれている様々な事実を確認することです。

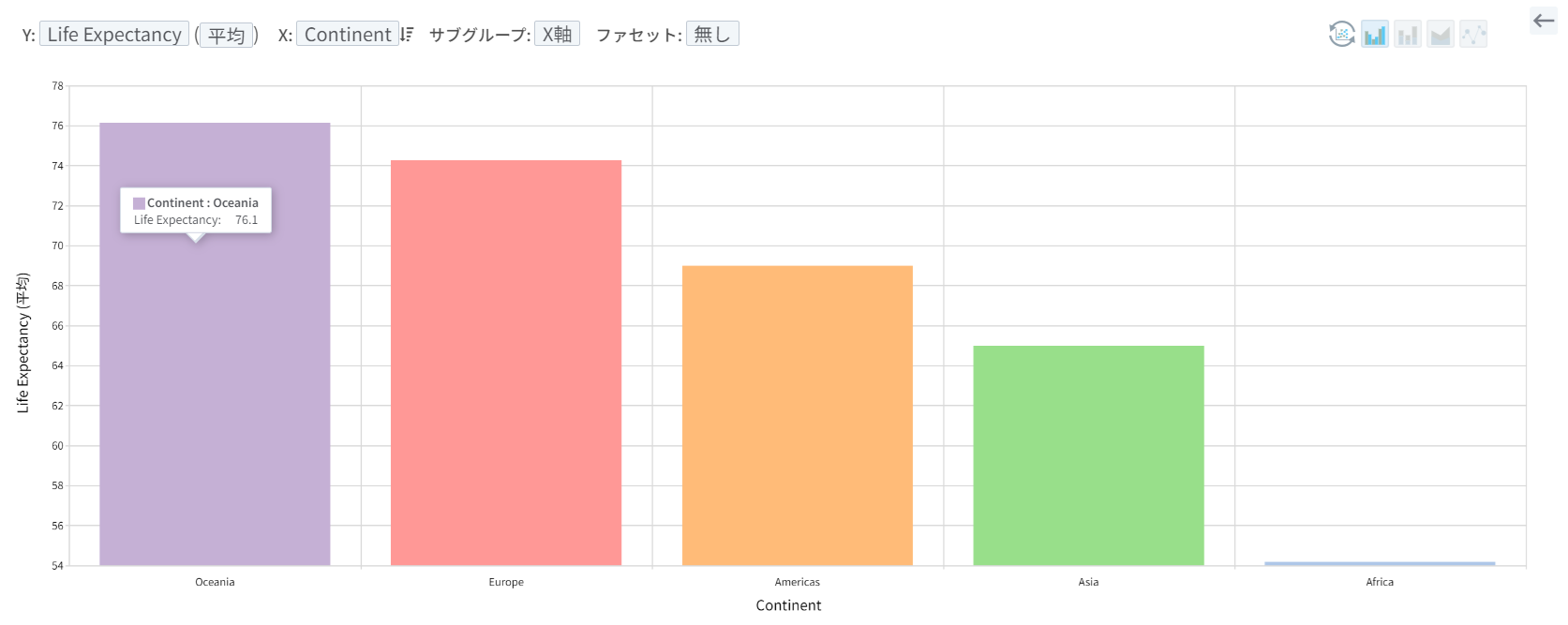
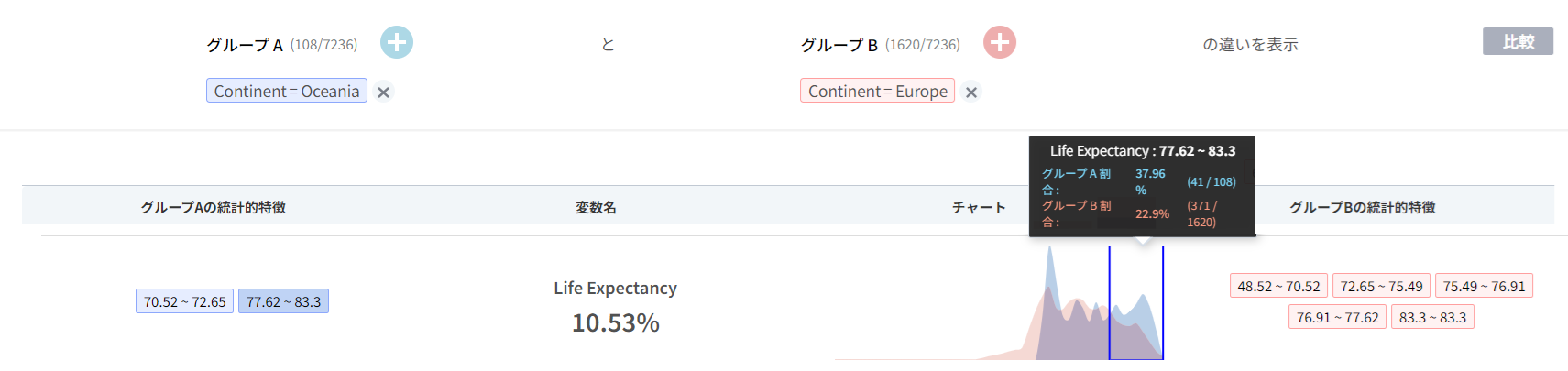
以下は、Hans Roslingのデータを使用して主要な大陸の1962年～2015年の平均寿命を平均値でまとめた棒グラフです。オセアニア大陸が76.1歳で平均寿命が最も高いという「事実」を確認することができます。

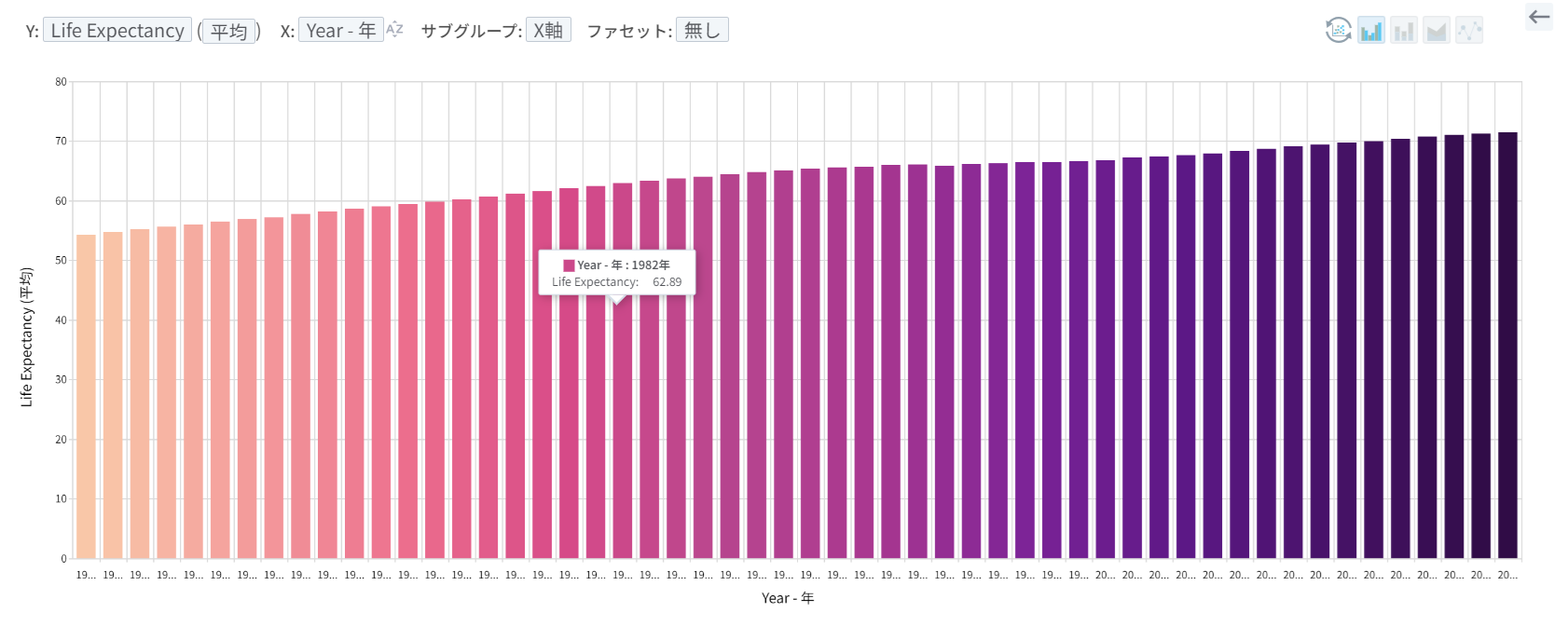
時間の経過に伴って、人類の平均寿命も着実に伸びてきたという「事実」も確認することができます。

異なるグループ(国別、年別)間の平均を比較すると、必然的に差が生じますが、この差が有意な差であるのか、偶然の結果であるのか、差がどこから来るのかなどの質問に答えるには、平均値を比較することからさらに一歩進んでいく必要があります。

Exploratory Analytics (探索的分析):

通常、EDA (Exploratory Data Analysis)と呼ばれる探索的分析は、視覚的な分析テクニックやツールを活用して、データの形状、分布、変数間の関係をグラフや基本的な統計値(相関係数、信頼区間など)を活用して確認することです。

分析モデルを活用してデータに含まれる一般化が可能なパターンを探すデータモデリング(推論、予測分析、仮説検証など)作業をするのではなく、偏見なくデータを隅々まで見て、これまで疑問に思っていたことを定量的に確認して、その確認する過程で新たなインスピレーションを受け、また、新たな疑問も抱くようなプロセスです。

探索的分析と記述分析の手法の間に厳密な境界があるというよりは、探索的分析が伝統的な記述分析にモダンな視覚的な分析を組み合わせることで記述分析の有用性と自由度を高めたと理解する方が正しいと思います。

EDAの現在の概念と手法を完成させた John W. Tukeyの言葉を借りると、「EDAは、存在すると信じていること、または存在しないと信じていることをデータから(視覚的に)探し出そうとする柔軟な態度であり、意志である」。

“‘Exploratory data analysis’ is an attitude, a state of flexibility, a willingness to look for those things that we believe are not there, as well as those we believe to be there.” by John W. Tukey

EDAの用途 1. データの分布から有意な違いを発見する

大陸間の平均寿命を要約値(平均)ではなく、分布(下図は箱ひげ図)を通して比較すると、平均値では隠されている不確実性(uncertainty)が見えてきます。オセアニアの場合、平均寿命が比較的狭い範囲に密集しているのに対し、ヨーロッパの場合、平均寿命が低いレコード(点で表現)が下方に広く広がっていることを肉眼で確認することができます。

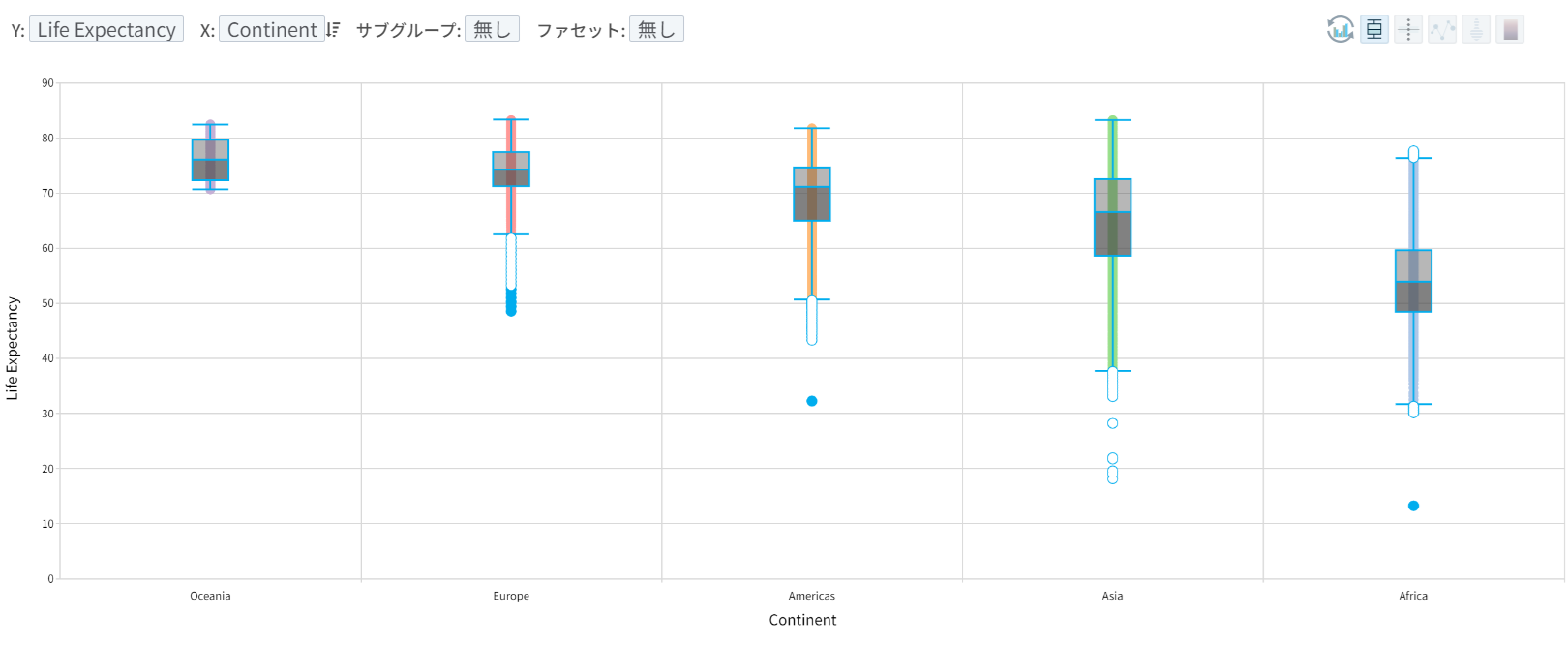
• 平均値だけを見ても、オセアニア大陸とヨーロッパ大陸の間で平均寿命に差があると確定的に答えることができます。それは事実です。ただし、2つのグループ間の平均値に意味のある違いがあるかという質問に回答するためには、2つのグループの分布も合わせて考慮する必要があります。
• 分布を見ると、平均の背後に隠れている個々のレコードの不確実性(変動性、variation)が明らかになり、与えられた質問に対して確定的ではなく、確率的に答えなければなりません。
• 次に、同じ分布を箱ひげ図ではなく、95%の信頼区間(confidence interval)で比較してみましょう。実務的な観点では、異なるグループ間で95%の信頼区間が重ならない場合は、その2つのグループ間の平均値に有意な差がある(=差が偶然に発生したものではない)と言うことができます。

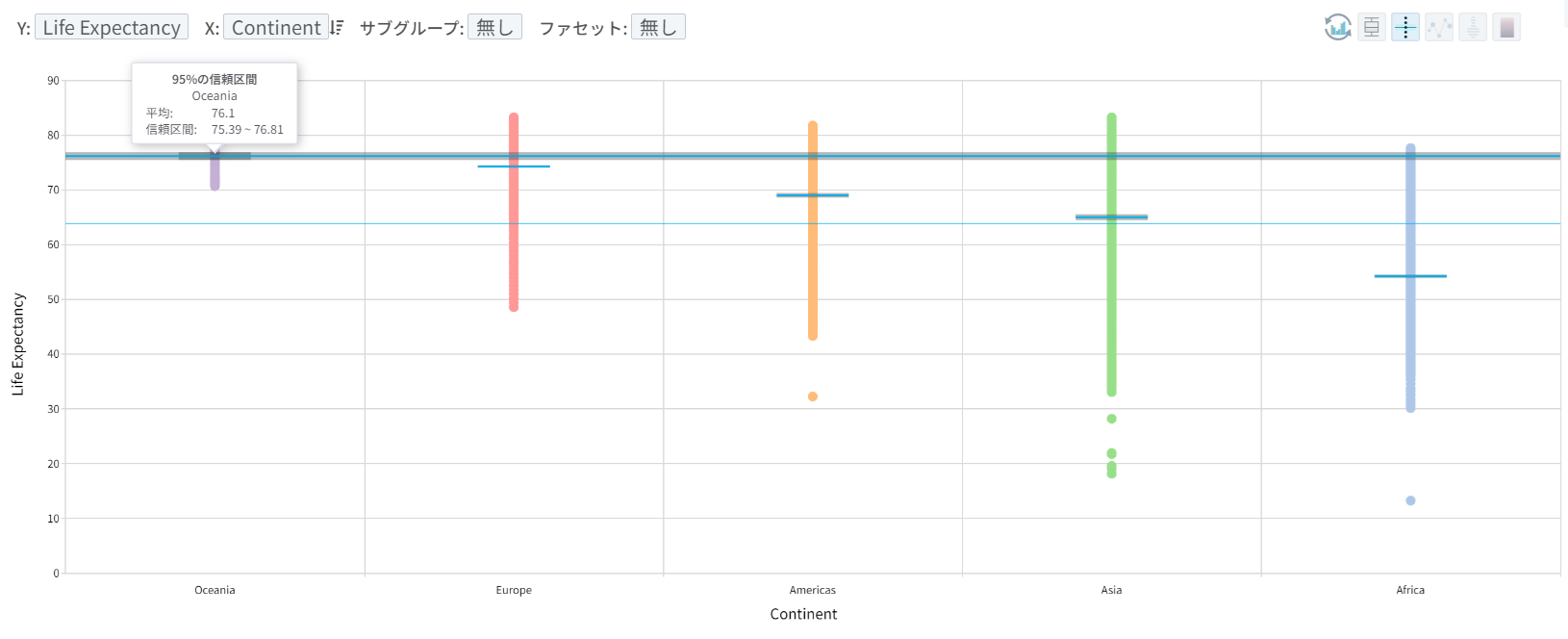
• 信頼度(90％、95％、99％)が高くなると信頼区間の幅が広くなり、同じ信頼度でもサンプルサイズが小さいほど信頼区間が広くなります(不確実性が大きくなります)。ほとんどの教科書や統計ツールでは、信頼区間は t分布に基づく公式を使用して計算されますが、最近では改善したコンピュータ計算能力を活用して bootstrap方式で計算することもあります。
• ほとんどの人は95%の信頼区間は「真の値(架空/想像上のグループの真の平均値)がその区間内にある確率が95%である」ということを知っていますが、これは事実と異なります。真の平均値(true mean)は私たちが知らないだけで、すでに決まっているはずなので、特定の区間にその値が存在する確率は 100% もしくは 0% であって、95%であるはずがありません。
• 95%の信頼区間の正確な意味は、母集団から同じ方法でサンプリングをした後に、信頼区間を計算する作業を無限に繰り返す場合に、計算された信頼区間のうち95%程度が真の平均値を含むことになるという話です。
• 同様に、2つの大陸の平均寿命を確率密度のグラフ(Probability Density Plot)で比較すると、ヨーロッパ人の平均寿命がオセアニア人の分布と比較して左に偏っていることが確認できます。

EDAの用途 2. 変数間の相関関係を確認する

平均寿命が他の変数とどのような関係を持つかを調べることもEDAの役目です。平均寿命(Y)と1人あたり所得(X)の2つの変数を以下のように散布図(scatterplot: 個々のレコードをX、Y座標上に散らして表現する視覚化方法)で表現して、2つの変数間の相関関係を確認することができます。

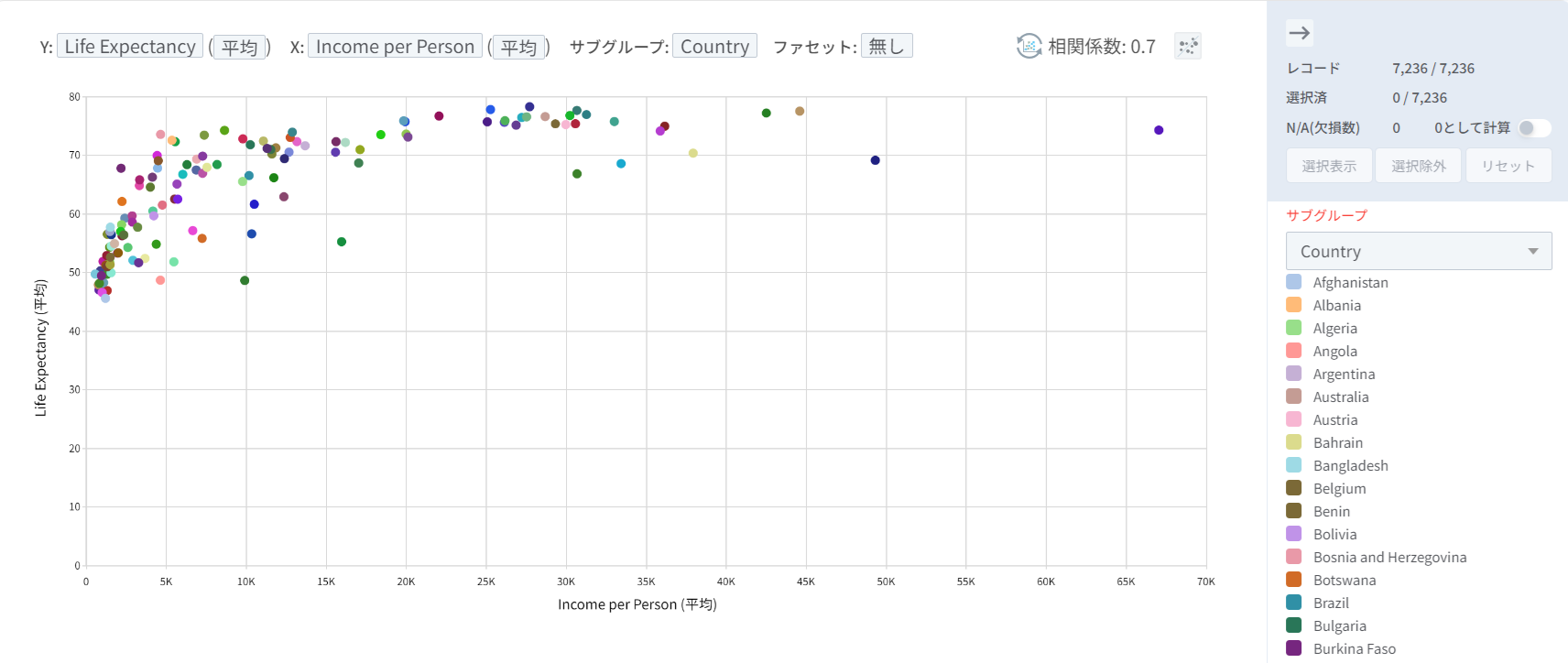
以下は、平均寿命(Y)と1人あたり所得(X)の関係を国単位でまとめて(下図ではサブグループで表示)、視覚化した結果です。データセットには、個々の国のレコードが合計54件(1962～2015年、各年度ごとに1件ずつ)あり、国別の54個の観測値を1つの平均値に要約・集計(aggregation)して1つの点として表現したグラフです。「平均所得が高い国ほど長生きする傾向がある」と言えます。

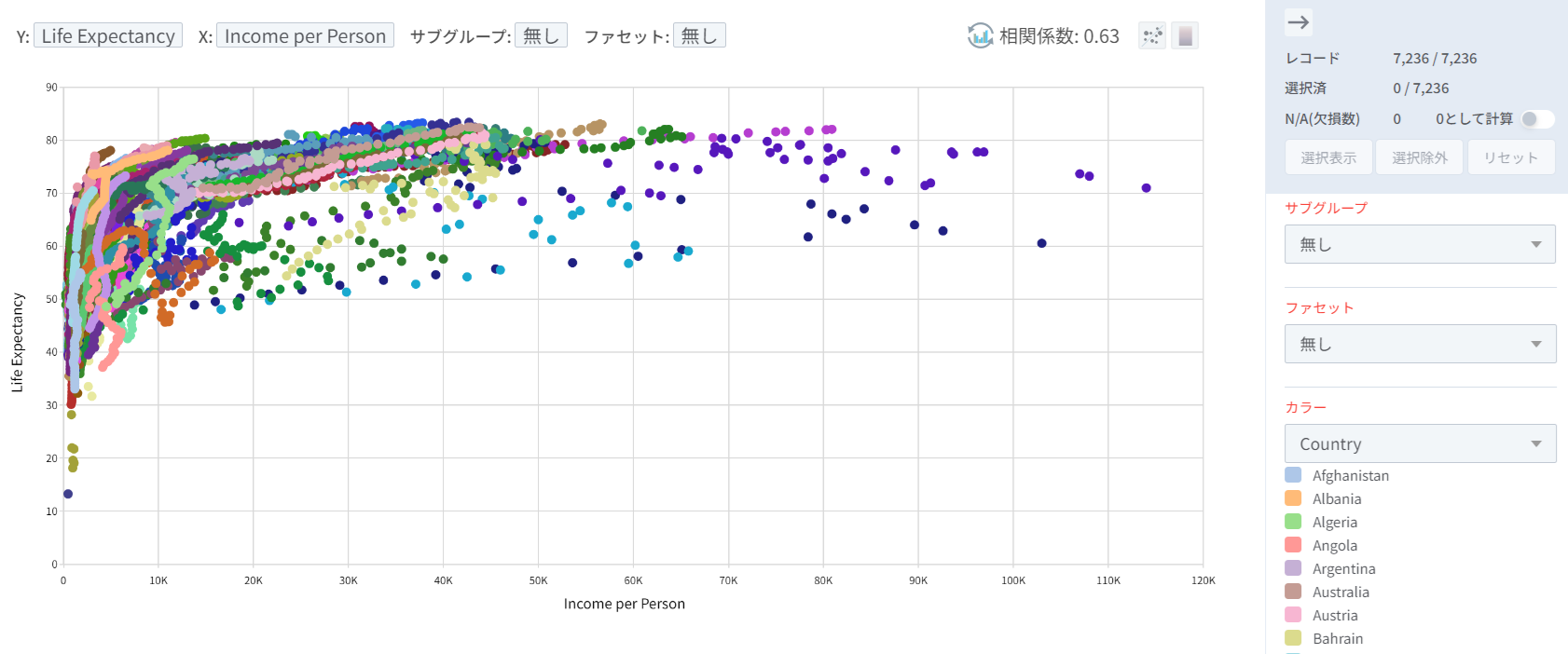
次に、国別にレコードをまとめていたルール(サブグループ: Country)を除外して、個々のレコードを表示する形で視覚化してみましょう。やはり、所得水準が高くなるにつれて平均寿命も上昇する関係(正の相関関係)が見られます。

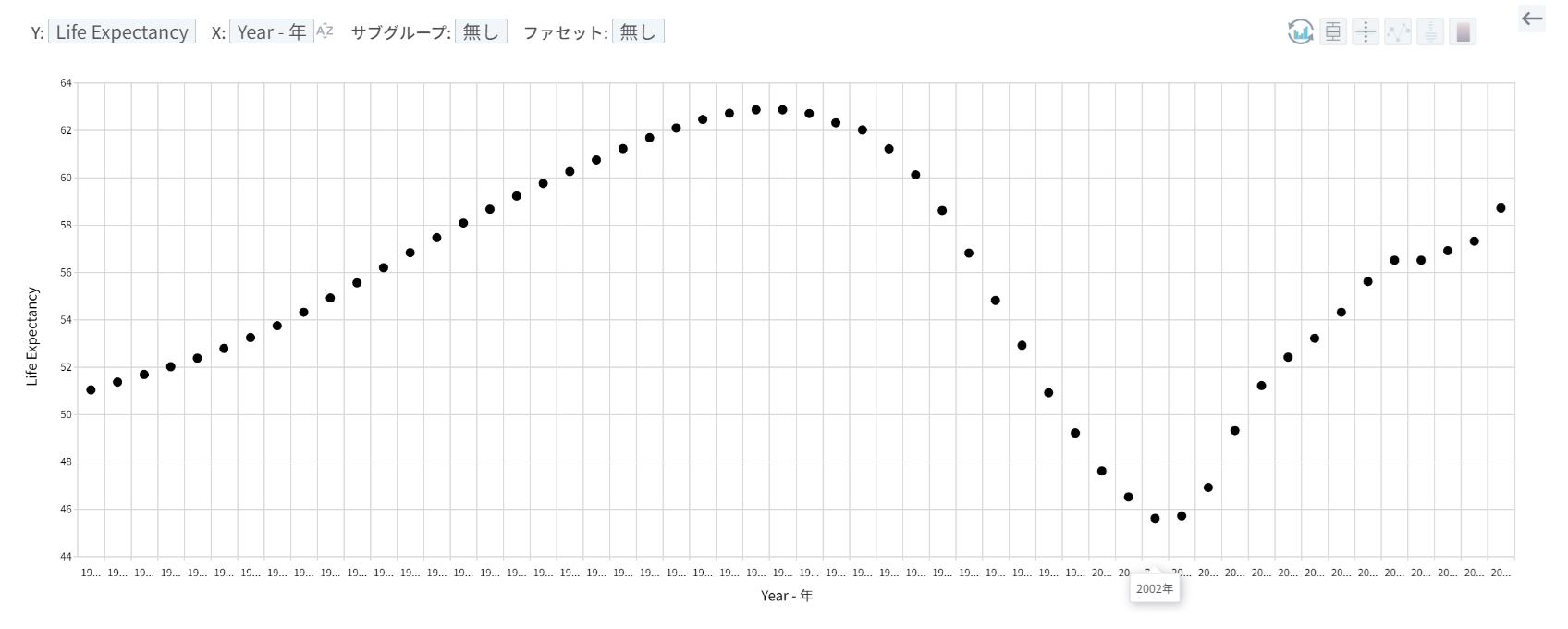
次に、個々の国別に分けて見てみましょう。(右側にある個々の国名をクリック) 特定の国(ボツワナ(Botswana))では、線形的な正の相関関係ではなく、例外的な(非線形的な)パターンが見られます。

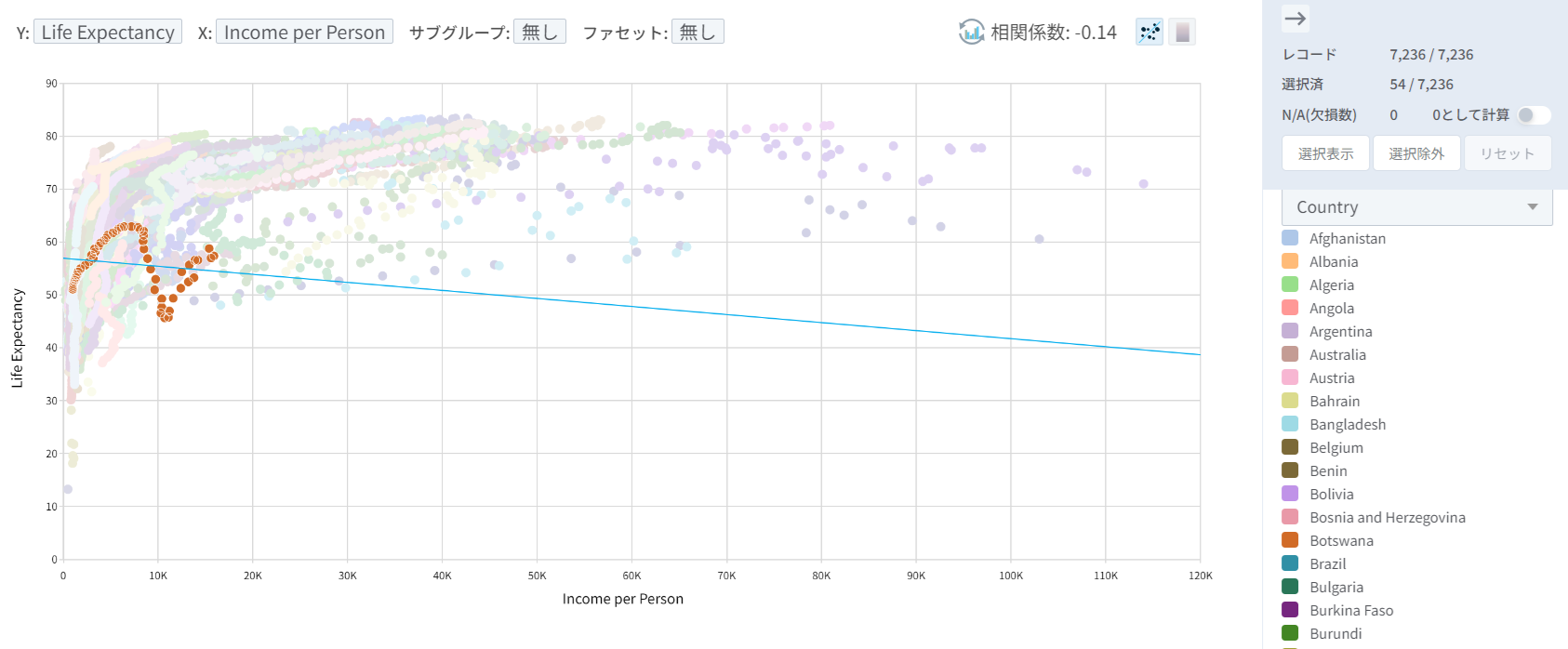
ボツワナのみを切り離して平均寿命を時系列で見てみましょう。おそらく1人あたり所得の増加による平均寿命の上昇の効果を相殺するような他の国家的な災害があったと推測できます。(正確な原因は我々が確保したデータでは不明)

Appendix. データ分析のタイプ

• 記述分析と予測分析の違いは、分析テクニックや方法にあるのではなく、分析の目的にあります。同じ分析テクニックや方法によって作成したモデルを予測用途で活用することも、記述用途で活用することもできます。
• 記述分析は、分析の目的が予測による意思決定の自動化にあるのではなく、データから現象についてより正確で深い説明を見つけ出し、より良い意思決定を行うことにあります。
• 推論分析は、比較的少ないサンプルデータから発見したパターンを集団全体(母集団、現実世界全体)に対して一般化するために、伝統的な統計技法(p値、何らかの検定など)を使用することです。データが比較的一般的なものとなった昨今では、その有用性は相対的に低下していますが、自分が発見したパターンに疑問を抱いている人々を「統計的に」説得するために活用することができます。
• 因果分析は技術のみで可能ではなく、現実の動き方に対する知識と信念に基づいて、RCT (ランダム化比較試験)や Conditioning (コンディショニング)などの分析手法で因果性を探す分析手法です。最近では、実験データ(RCT)ではなく、観測データを用いて因果関係を探す研究が活発に行われています。