平均は合っているのにおかしい理由:集計の罠
集計の罠:部分は良いのに全体は悪い事例
データ分析でよく使われる「平均」は、最も身近で馴染みのある代表値です。しかし、場合によっては重要な事実を隠したり、誤解を招いたりすることがあります。
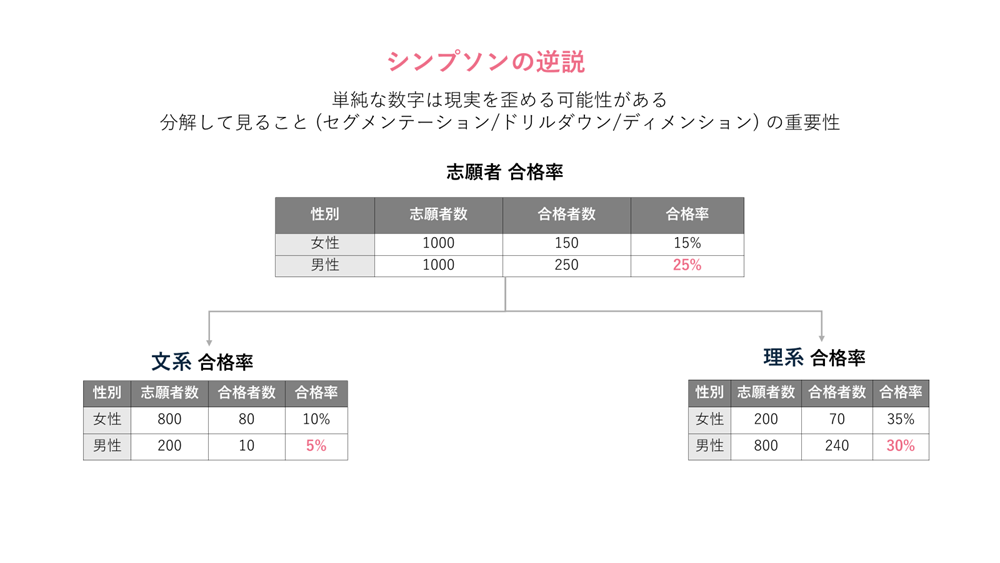
例えば、男女別の合格率が男性25%・女性15%だったと仮定してみましょう。ダッシュボードで平均値だけを見れば、「男性の合格率が高い」と判断しがちです。
しかし、このデータを学部ごとに分けてみると状況は一変します。
- 文系学部では女性の合格率が10%で、男性(5%)より高い
- 理系学部でも女性35%・男性30%と、女性の方が高い
なぜ平均値だけを見ると逆の印象になったのでしょうか?
ヒントは「合格者数」にあります。
さらにもう1つ例を挙げましょう。マーケティングのCAC(顧客獲得単価)分析でも似た問題が起こります。企業全体の平均CACは一見問題なさそうに見えます。しかし、チャネル別に分解してみると、特定のチャネルでは1人の顧客を獲得するコストが利益を上回り、実は赤字になっているケースもあります。これも平均値に頼りすぎることで見逃してしまう典型例です。
シンプソンのパラドックスとは?
このように、平均値や割合といった統計指標が、下位グループに分けたときに逆転現象を起こすことを「シンプソンのパラドックス(Simpson’s Paradox)」と呼びます。
部分ごとに見れば決して間違いではないのに、全体を合算すると結論が真逆になり、代表値が実際の文脈を歪めてしまうことがあるのです。
データを基に現象を正確に把握し、ビジネスの意思決定に活かしたい実務者にとっては、「平均値の落とし穴」を理解し、データをさまざまな切り口(多次元)で分解して見る習慣が欠かせません。
今回の記事を通じて、単なる平均にとどまらず、データの本当の意味をより深く読み解ける実務者に一歩近づけることを願っています。
なぜ私たちはいつも平均を見たのですか?
平均は簡単でおなじみ
平均値は、計算が簡単で直感的に理解しやすい指標です。多くの人が慣れ親しんでおり、複雑な説明が不要なため、データ分析の結果を共有したり報告したりするときに頻繁に使われます。
ダッシュボードも同様に、複雑なデータをシンプルに視覚化して表現することで、現場の実務者が直感的に理解・活用できるようサポートします。このとき、平均値のような集計指標が大きな役割を果たしています。
さらに、Excelでも選択したセル範囲の平均値が自動表示されるなど、平均は多くのデータを最も手軽に理解できる指標として定着しています。
平均は間違っていませんが、歪む可能性があります
外れ値が平均値を歪める仕組み
平均値の最大の欠点のひとつは、極端な値(外れ値)に非常に敏感だということです。例えば、あるバスに乗っている乗客の平均年収を計算したとしましょう。そこにビル・ゲイツが1人乗り込んだ瞬間、平均年収は一気に跳ね上がります。このように、極端な値がサンプルに含まれると、平均値は全体データの代表性を失ってしまうのです。
なぜ分布も一緒に見るべきなのか?
「平均だけを見るな、分布も確認せよ」
これはデータ分析者の間でよく語られる格言です。
というのも、単にまとめられた平均値だけでは、個々のデータがどの位置にあるのか、つまりデータの広がりや形状を把握することはできません。
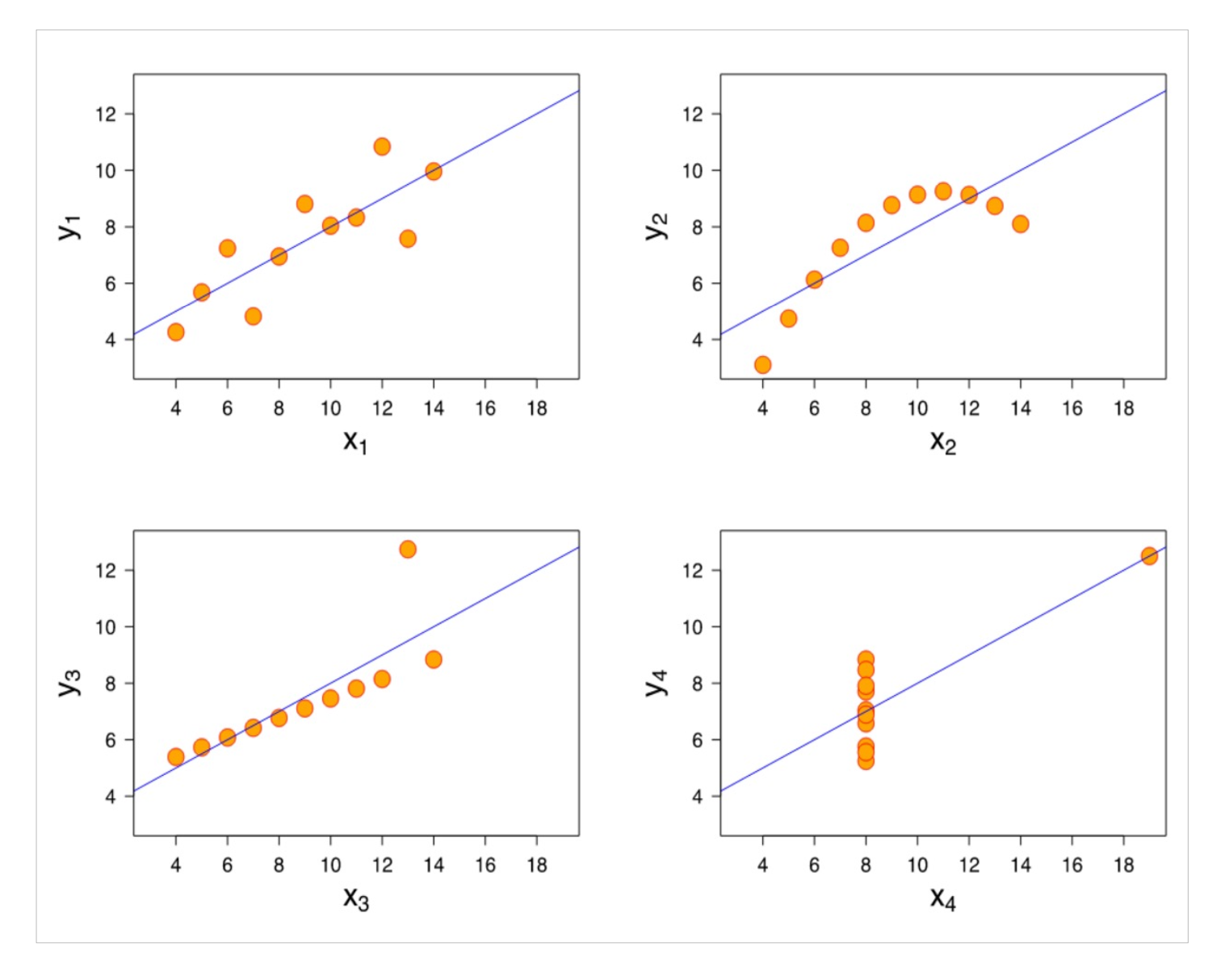
統計学の有名な例とし「アンスコムのクァルテット(Anscombe’s Quartet)」があります。これは、同じ平均・分散・相関係数を持つ4つのデータセットが、グラフ化すると全く異なるパターンを示すというものです。
このように、分布を合わせて確認することは、データの本質的な特徴を捉えるために欠かせません。
そんな時こそ“中央値”の出番
中央値が示すものとは?
中央値(Median)とは、与えられたデータを大きさの順に並べたとき、ちょうど中央に位置する値のことです。
中央値は、平均値と違って極端な値(外れ値)の影響を受けにくいのが特徴です。そのため、データ全体の“中心的な傾向”を把握するのに有効です。
中央値が平均より優れているケース
平均値は、極端な値(外れ値)によって簡単に歪められてしまうことがあります。一方、中央値はデータの中心的な傾向をより正確に表すことができます。
例えば、所得分布や不動産価格のように、一部に極端に大きな値が含まれるデータでは、平均値は実態とかけ離れてしまうことが少なくありません。
このような場合、中央値の方がデータセット全体の「一般的な傾向」をより的確に示してくれます。
平均 と 中央値、いつどちらを見るべきか?
正規分布 vs 歪みのある分布
データの分布が左右対称の正規分布に近い場合、平均値と中央値はほぼ同じになります。そのため、このようなケースでは平均値を使っても問題ありません。
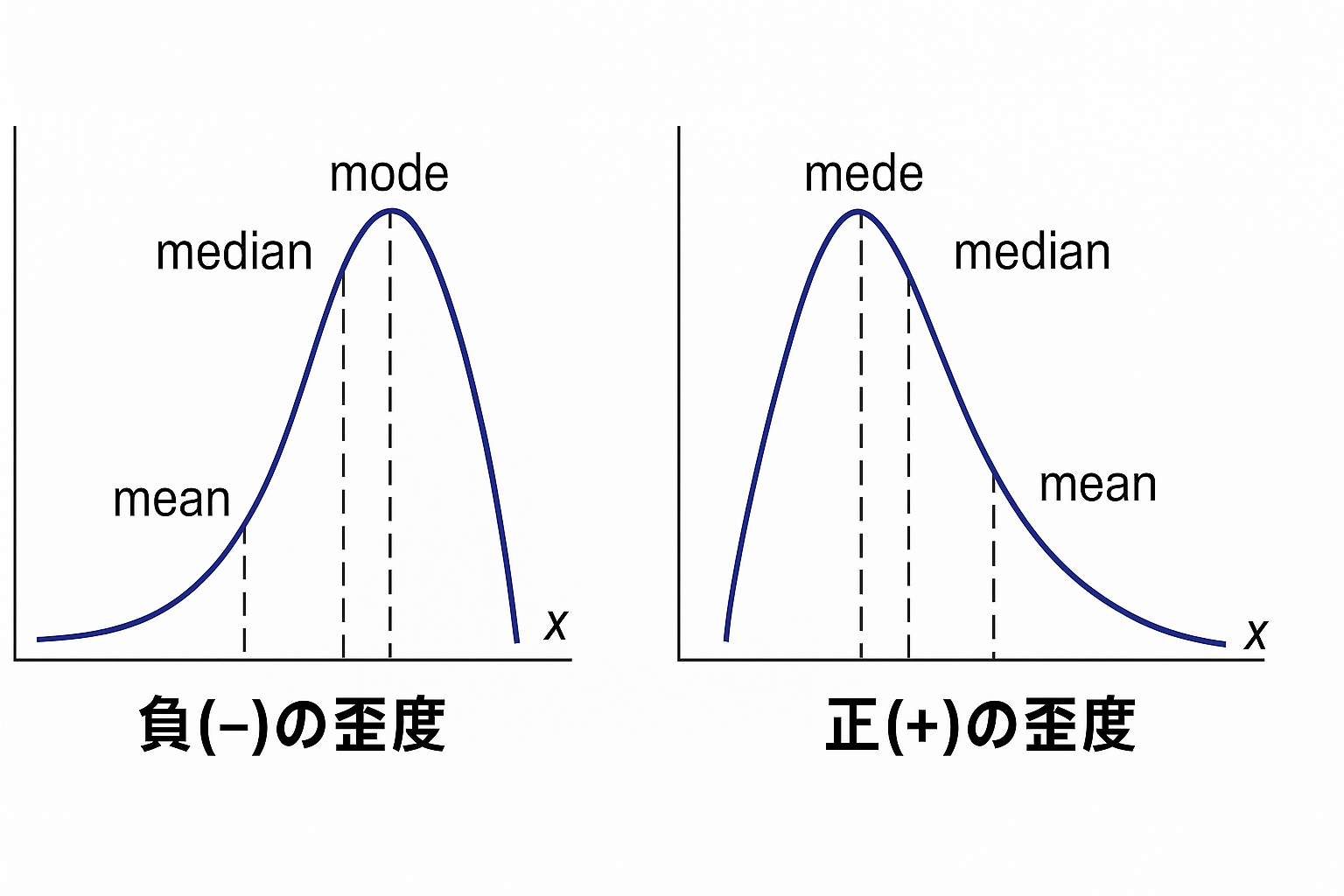
しかし、所得分布のように一方向に尾が長く伸びる歪み(スキュー、skewness)のある分布では事情が変わります。
この場合、極端な値が平均値を一方向に引っ張り、全体の傾向を歪めてしまうのです。
このような状況では、中央値の方がデータの“中心”をより適切に表す代表値になります。
代表値選択基準
- 平均:データが正規分布に近いか、極端な値の影響をあまり受けない場合。すべてのデータ値の情報を活用する場合。
- 中央値:データに極端な値が存在したり、分布が一方に偏っている場合。データの「中間」点を把握することが重要な場合。
必ずしも中央値だけを見なければならないのか?
最頻値の概念と活用例
最頻値(Mode)は、データセットで最も頻繁に出現する値を意味します。例えば、アンケートで最も多く選択された回答や、衣料品の販売で最も多く売れたサイズなどを表すのに便利です。最頻値は主にカテゴリ型データや特定の値が集中して現れる場合に活用されます。
3つの代表値を一緒に確認する
平均、中央値、最頻値を一緒に考慮することで、データの特性を包括的に理解することができます。1つの代表値だけではデータの全体像を把握することは難しいため、3つの値をすべて見て、データがどのように分布しているのか、極端な値の影響はないのかなどを把握することで、より正確なインサイトを得ることができます。
例えば、商品別の返品率データを見ると、平均は15%ですが、中央値は8%、最頻値は5%かもしれません。この場合、平均値だけを見ると「私たちは返品が多い」と判断できますが、実際には半分以上の商品は返品率が10%未満で、最も多い返品率は5%なので、問題は一部の特定の商品やケースに集中していることがわかります。
このように、3つの代表的な値を一緒に見ると、「どこが問題なのか」まで見えてきます。
箱ひげ図: 数値を視覚的に一目で確認する
箱ひげ図の構成要素の説明
ボックスプロットは、データの分布をひと目で把握できる強力な可視化ツールです。データの中心やばらつき、外れ値(極端な値)などを簡単に確認することができます。
ボックスプロットは主に次の要素で構成されています:
中央線(Median)
データの中央値を表します。ボックス内に引かれた線がこれにあたります。
ボックス(箱)
データの中央50%が入る範囲です。下側の線が第1四分位数(Q1)、上側の線が**第3四分位数(Q3)**を示しています。
ひげ(Whiskers)
箱の外に伸びる線で、外れ値を除いたデータの最小値・最大値を示します。
外れ値(Outliers)
ひげの外に点で表示され、通常のデータの範囲から外れた極端な値です。
このようにボックスプロットは、データの中心・広がり・外れ値まで一度に確認できる便利なグラフです。
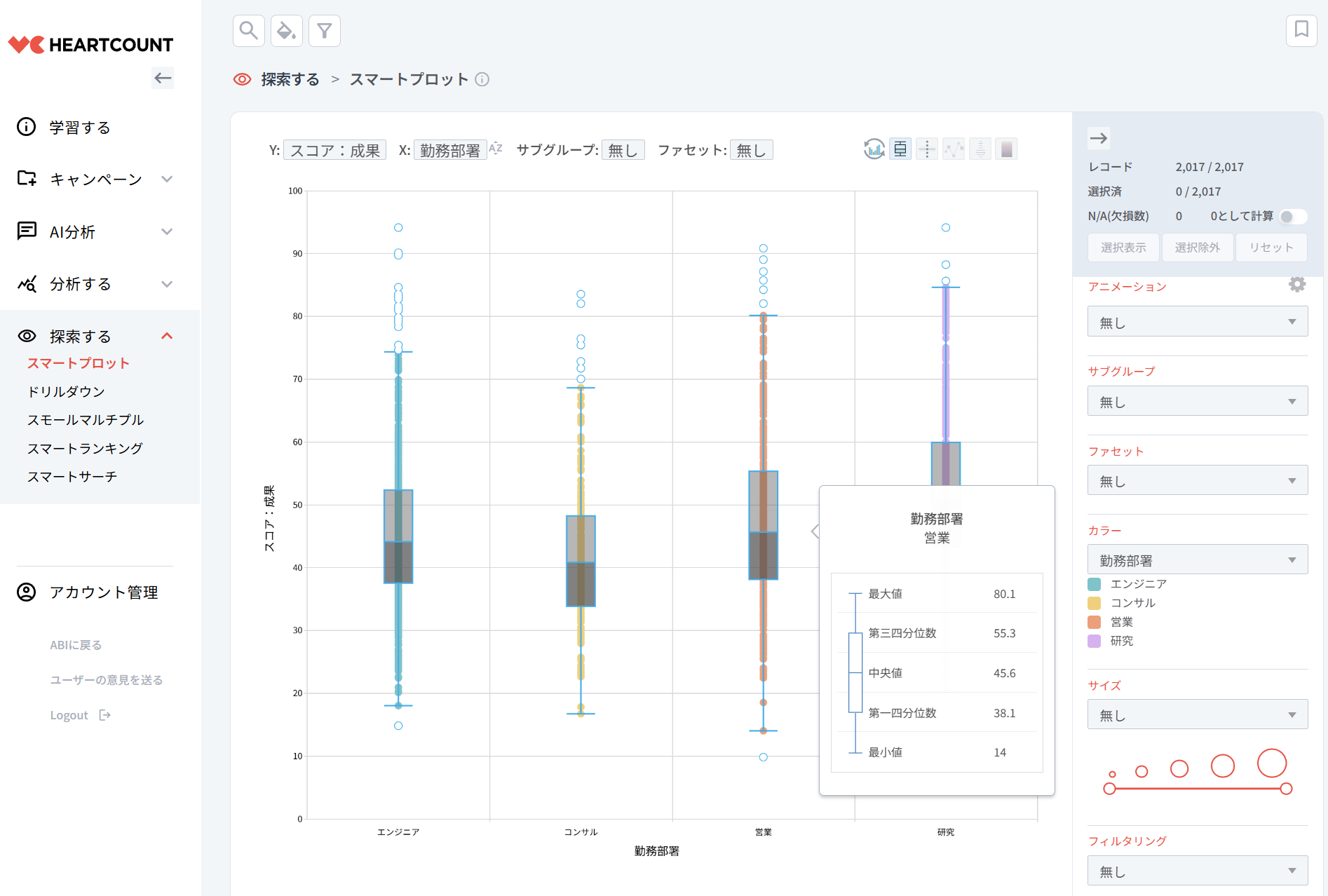
箱ひげ図で見るインサイト
箱ひげ図を使えば、データの中心傾向・散らばり具合(分布)、対称性、そして外れ値の有無を簡単に把握できます。
複数のグループの箱ひげ図を並べて比較することで、各グループ間の相対的な違いや分布の特徴を直感的に理解することができます。
例えば、広告チャネル別のROASを箱ひげ図で描くと、平均は似ていても、あるチャネルは収益が安定的で一貫しているのに対し、別のチャネルは極端に高いROASのデータが全体の平均を引き上げているだけで、多くは損をしている構造だと視覚的にわかります。
数字だけでは見えなかったリスク要因が箱ひげ図では浮き彫りになるのです。
実務ですぐに使える代表値解釈のヒント
Excelで平均・中央値・最頻値を求める方法
Excelでは、基本的な関数を使うだけで平均値・中央値・最頻値(モード)を手軽に求めることができます。
平均値を求める関数
=AVERAGE(範囲)
指定したセル範囲の平均を計算します。
中央値を求める関数
=MEDIAN(範囲)
データを昇順に並べたときの真ん中の値を返します。
最頻値(モード)を求める関数
=MODE.SNGL(範囲)
指定した範囲で最も頻繁に出現する値を返します。
さらに、ピボットテーブルのようなExcelの集計機能を活用すれば、データを効率的に要約・分析することも可能です。大量データでも簡単にグループごとの平均や合計を算出できるので、業務効率がぐっと上がります。
データ数が少ない場合、中央値の解釈に注意!
中央値は、データを大きさ順に並べたとき必ず存在する指標です。つまり「中央値が存在しない」ということはありません。
ただし、データの数が極端に少ない場合は、中央値ひとつだけで全体の傾向を判断するのは難しいことがあります。
例えば、データがたった3つしかない場合、中央値がそのデータ全体の傾向を代表しているとは言いにくいでしょう。
このようなときは、他の代表値(平均・最頻値など)やデータ全体の文脈をあわせて考慮する、またはより多くのデータを集めて分析することが重要です。
代表値は「数字」ではなく「視点」
データ解釈は「人の思考」から始まる
データは現象の「何が起きているか(What)」を示してくれる強力なツールです。しかし、多くの場合データそのものが「なぜそれが起きたのか(Why)」という原因を直接教えてくれるわけではありません。
そのため、実務でデータを扱う人は次のような姿勢が求められます。
- 鋭い問いを立てる
- 問題を構造化する
- 仮説を立てて検証する
このようなプロセスを通じて初めて、データの奥に隠れている「本当に役立つ新しい気づき」を引き出すことができます。
- データはあくまで現象の一部を切り取ったものに過ぎない
- 解釈の質は分析者の思考力と問いの立て方で決まる
平均を超えるための実務者の目線
単に数字を並べたり要約するだけでなく、データの分布を深く読み解き、さまざまな代表値(平均・中央値・最頻値など)を適切に活用することは、実務者の分析的思考力を一段と高めるための重要なステップです。
この力は、データを通じて組織の意思決定を改善し、ビジネスの成長を支えるコアコンピテンシー(中核的能力)になります。
一緒に読むと役立つ記事