[因果推論1] Potential Outcome Framework (潜在的結果フレームワーク)

はじめに: 潜在的結果フレームワークとは

データ分析において、因果推論は分析の論理的な流れに自然に従う思考の流れに対する答えになります。単に「What」の質問に対してSQLで作成したサマリテーブル的な回答だけでは、実際にデータを作成したデータ生成過程について綿密に把握できない場合が多いです。そこで、数学/統計/経済学者は絶えず「経済的効果」ということを明らかにするために、つまり「Why」の質問に対する回答をすることができる体系的な数学的方法論、つまり因果推論の方法論を確立してきました。

潜在的結果フレームワーク(Potential Outcomes Framework)は、その方法論の一つです。潜在的結果フレームワークの最大の利点(?)は、因果推論というものがどのようなものなのかという脈絡をつかむのに最も効果的であるということです。複雑に絡み合ったデータからどのように因果関係を把握するのかについて直感的で理解しやすい方法論です。

ランダム化比較試験(RCT) - A/Bテスト

潜在的結果の話をする前に、まず、ランダム化比較試験(RCT)についての話をしましょう。RCTは因果性を把握する上で、常に最優先される方法論です。

ある政策/イベント(例: 出産奨励政策)の因果性(効果、例: 政策実施後の出生率に及ぼす影響)を測定したい場合、その政策の受益者vs非受益者を対象に、政策実施前と実施後をそれぞれ比較すればよいと思います。政策の恩恵を受けたグループとそうでないグループの指標に明確な差が存在する場合、これは政策に明らかな効果があったと言えます。

しかし、実際にはそうでない場合がほとんどです。なぜなら、現実の世界ではほとんどいつも、このような方式の推論を不可能にする要因が存在するからです！

研究者のバイアスが知らず知らずのうちに介入したり(無意識のうちに効果がありそうな人に政策の恩恵を与えたり)、受益者の他の要因によって指標の変化が発生する可能性も存在します(単に時間が経つにつれて変化したとか、健康関連の政策であれば、政策のためではなく、ただ運動を頑張ったからそうなったとか)。

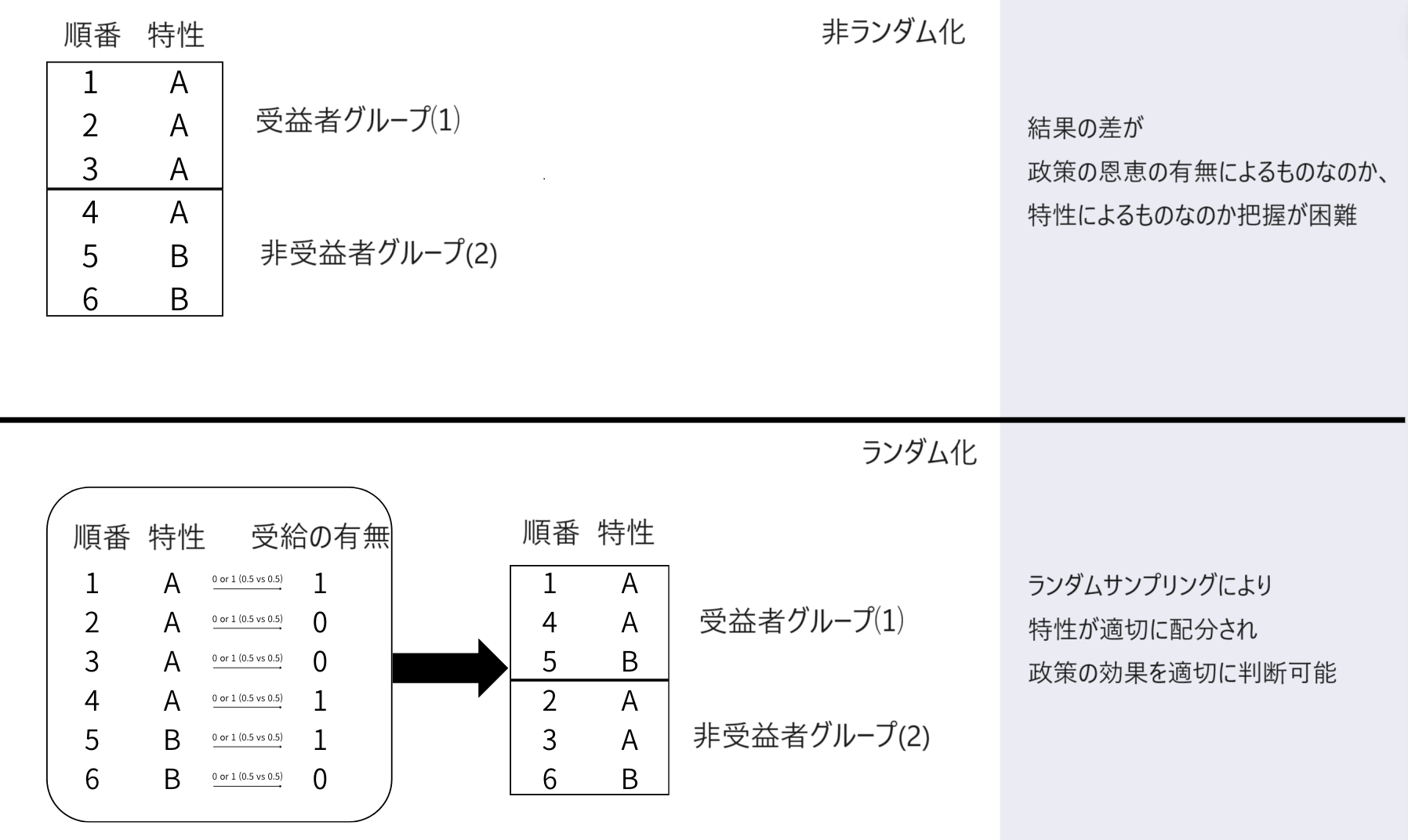
RCT(A/Bテストと呼ばれます)はまさにそのような要素の不確定性をかなり相殺してくれる良い方法です。なぜそうなのかについて直感的に考えてみると... 全体のグループを受益者グループ/非受益者グループにランダムに分けたとします。

全体を同じ確率でランダムに2つのグループに分割することは、全体のグループに属する各個人に0または1のタグを付ける作業としても理解することができます。このとき、各個人が0または1に属する確率は、他の個人が0または1に属する確率と独立しているため、この作業を繰り返すと因果性を曖昧にする可能性のある要素が相殺され、各要素ができるだけ均等に分布することが期待できます。ただし、これは十分なサンプルサイズが保証される場合にのみうまく機能します(0と1を交互に選ぶ作業を5回のみ行うとすると、1-1-1-1-1が出る可能性もあるため...)。したがって、適切なサンプルサイズを知るためにPower Analysisを回すことになります。

因果推論の根本的な問題と潜在的結果(Potential Outcome)

問題は、このような種類の実験設計が常に可能ではないということです。多くの場合、すでに発生した過去のデータ(観察データ)からデータ生成過程を推論し、因果関係を把握しなければならないケースが発生します。この場合、必ず押さえておくべき問題、因果推論の根本的な問題(Fundamental Problem of Causal Inference)が発生します。

政策の話に戻りますが、どの政策が効果があったのかはどのように知ることができるのでしょうか。例えば、最近社会的にホットな問題である出生率を増進するための政府の新しい政策があり、政策が実際に出生率増進に効果があったかどうかを知りたいとします。その時、次の値を計算してみると良いでしょう。

(出生率政策の効果) =
(出生率政策の恩恵を受けた後の政策受益者グループの出生率) -
(出生率政策の恩恵を受ける前の政策受益者グループの出生率)

もし出生率政策の恩恵を受けた後、出生率が5%増加したとしたら、普通は気楽に「出生率が5%増加する効果があった」と言いがちです。ここで問題が発生します。「前後」という時間概念が導入されたためです。

時間概念の導入により、発生した値が政策の効果によるものなのか、それとも時間の流れの中でその政策の恩恵を受けたグループに介入した他の要因(突然、そのグループに属する家庭の父親が年度が変わって集団で昇進して給料が上がったなど)が原因なのかが不明確になります。それでは、時間概念を除いて計算式を再定式化してみましょう。

(出生率政策の効果) =
(出生率政策の恩恵を受けた場合の政策受益者グループの出生率) -
(出生率政策の恩恵を受けなかった場合の政策受益者グループの出生率(*仮定))

今回は「前後」の概念ではなく、同じ時間帯に、そのグループが政策の恩恵を受けなかったシナリオを想定してみましょう。もし、この状況で再びこの値を計算してみても、まだ5%の増加を示した場合、これは間違いなく政策の効果と言えます！なぜなら、同じ時間帯を想定することで、その時間帯の政策受益の有無を除く他のすべての要因をコントロールしたからです。

つまり、このシナリオでは、このグループは政策受益を除いたすべての条件が同等であることを意味します！

しかし、実際にはこの値は現実には求められません(出生率政策の恩恵を潜在的に受けなかった場合の政策受益グループの出生率)。そこで、「もしそうだったらどうだったのか」という意味で、私たちはこの値を潜在的結果(Potential outcome)あるいは反実仮想(Counterfactual)と呼んでいます。

Ceteris Paribus (ケテリス・パリブス)

それでは、政策の因果効果を推定することを諦めるべきなのでしょうか？そうではありません。ここで Ceteris Paribus が登場します。Ceteris Paribus は「他のすべてが等しい場合」を意味するラテン語です。政策の恩恵を受けたグループと最も類似したグループを見つけ、そのグループの出生率と政策の恩恵を受けたグループの出生率を比較することです。

(出生率政策の効果) =
(出生率政策の恩恵を受けた場合の政策受益者グループの出生率) -
(政策非受益者グループのうち出生率政策の恩恵を受けたグループと最も類似したグループの出生率)

この式では、(出生率政策の恩恵を受けなかった場合の政策受益グループの出生率) を (政策非受益グループのうち出生率政策の恩恵を受けたグループと最も類似したグループの出生率) に置き換えたことがわかります。両者の値は同じ値ではありませんが、それでも、非受益グループのうち、受益グループと最も類似したグループを見つけて、同じ期間の下で出生率を比較すれば、潜在的結果(Potential outcome)を推定することができます。したがって、できるだけ同等の条件の非受益グループを見つけることが重要な戦いになりますね。

理解を深めるために、ありそうもない例をもう一つ挙げてみましょう。

2つのサボテンを育てることになったとします。両方のサボテンは遺伝的な性質が同じです。育てる場所も同じ、日照量も同じ、鉢の種類も同じ、土の種類も同じです。2つのサボテン A、B のうち、A だけに水を少し多めに与えて、A と B のうちどちらがよく育つかを調べようとしたとします。

ところが、誤って B のサボテンの鉢をぶつけて倒して壊してしまいました！急いで別のサボテンを取り寄せ、同じ鉢に同じ土を入れ、B と同じ量の水を与え、同じ位置に置きました(これを B' と呼びましょう)。

ところが、B' の遺伝的性質は A と95%しか似ていません。残念なことに、A と B' を比較してみると、水を比較的多く与えた A の方がよく育ったとします。この場合、5％の差により「水を与えることはサボテンをよりよく成長させる効果がある」という絶対的な断言まではいかなくても、少なくとも道端の草の葉を与えて B の代替品にしたものよりは「効果があるようだ」という主張の裏付けの根拠として活用できるようになります。

結論とまとめ

上記の例における受益グループを処置群(Treatment group)、非受益グループを対照群(Control group)と呼びます。潜在的結果フレームワーク(Potential Outcome Framework)とは、反実仮想(Counterfactual)を置き換えることができる、処置群(Treatment group)と最も類似した対照群(Control group)を探す研究デザインを意味します。

参考資料