この記事では、現場で分析を行う実務担当者が無作為実験(A/Bテスト)なしでも因果関係を推定できるマッチング(Matching)手法を理解し、HEARTCOUNT AI分析を使って直接手を動かしながら学べるプロセスを紹介します。
イントロ
ある政策が実際にどのような影響を与えたのかを知りたい場合、最も信頼性が高い方法は無作為化比較試験(RCT, Randomized Controlled Trial)です。一般的にA/Bテストと呼ばれるこの手法は、因果効果推定の「ゴールドスタンダード」と見なされています。その理由は、この後の例でご説明します。
しかし現実には、倫理的・技術的な制約によってA/Bテストの実施が難しい場合が少なくありません。特にテック企業以外の一般組織では、実験環境が十分に整っていない、または整っていても全ての政策にA/Bテストを適用するには時間やコストの負担が大きすぎます。
こうした制約の中で、私たちは無作為実験を模擬(emulate)するためのさまざまな方法論を活用します。下記の「因果推論の階層構造」からもわかるように、RCTは最も信頼性の高い方法のひとつですが、それを代替・補完する手法も存在します。本記事では、その中でもマッチング(Matching)手法に焦点を当て、HEARTCOUNTのAI分析機能を活用して実際に手を動かしながら理解を深めていきます。
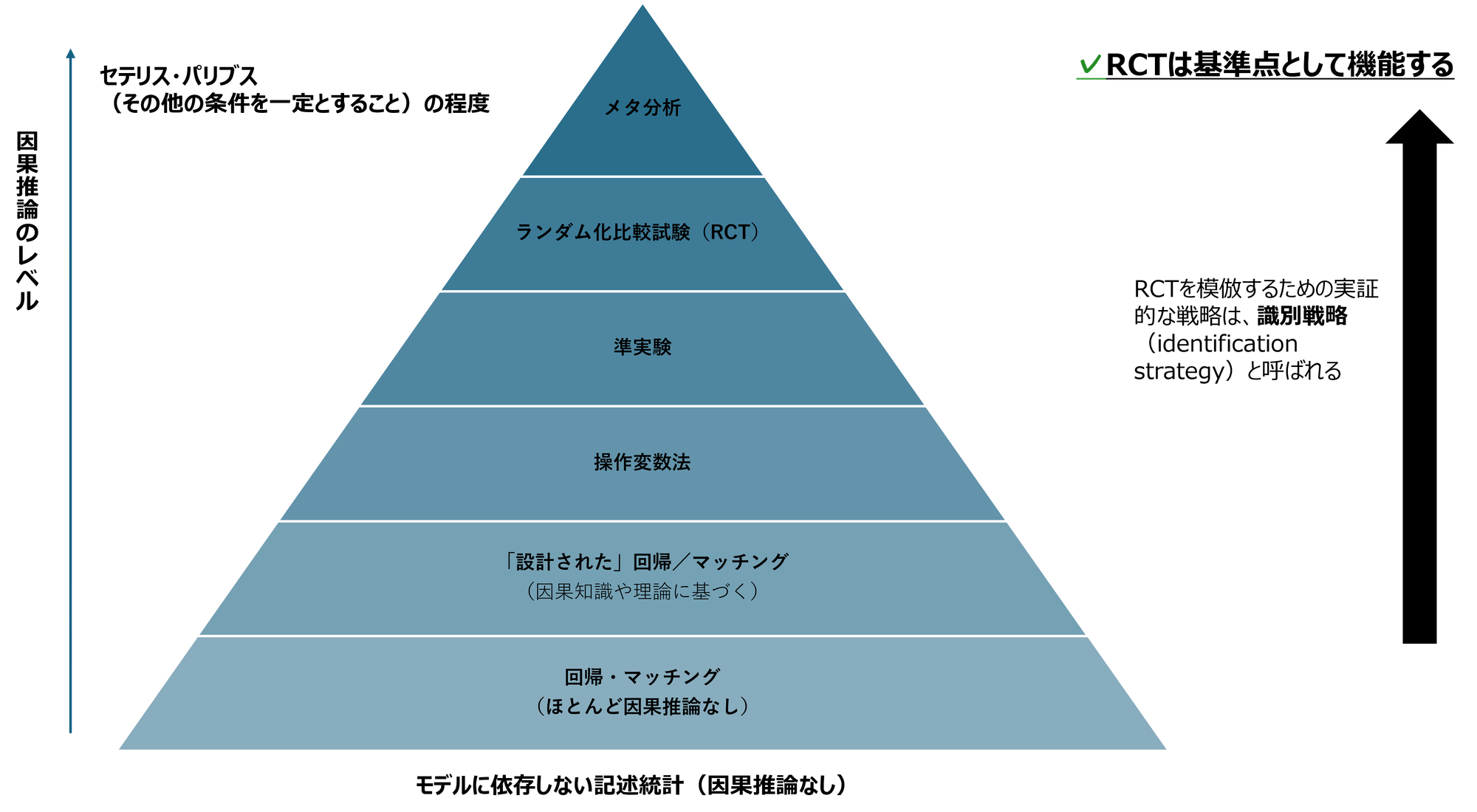
なぜA/Bテスト(RCT)がゴールドスタンダードなのか?
簡単な例で見てみましょう。
ある保険会社が社内研修を実施し、その研修が社員の収入にどのような影響を与えたのかを調べようとしています。
以下は研修を受けたグループのデータです。
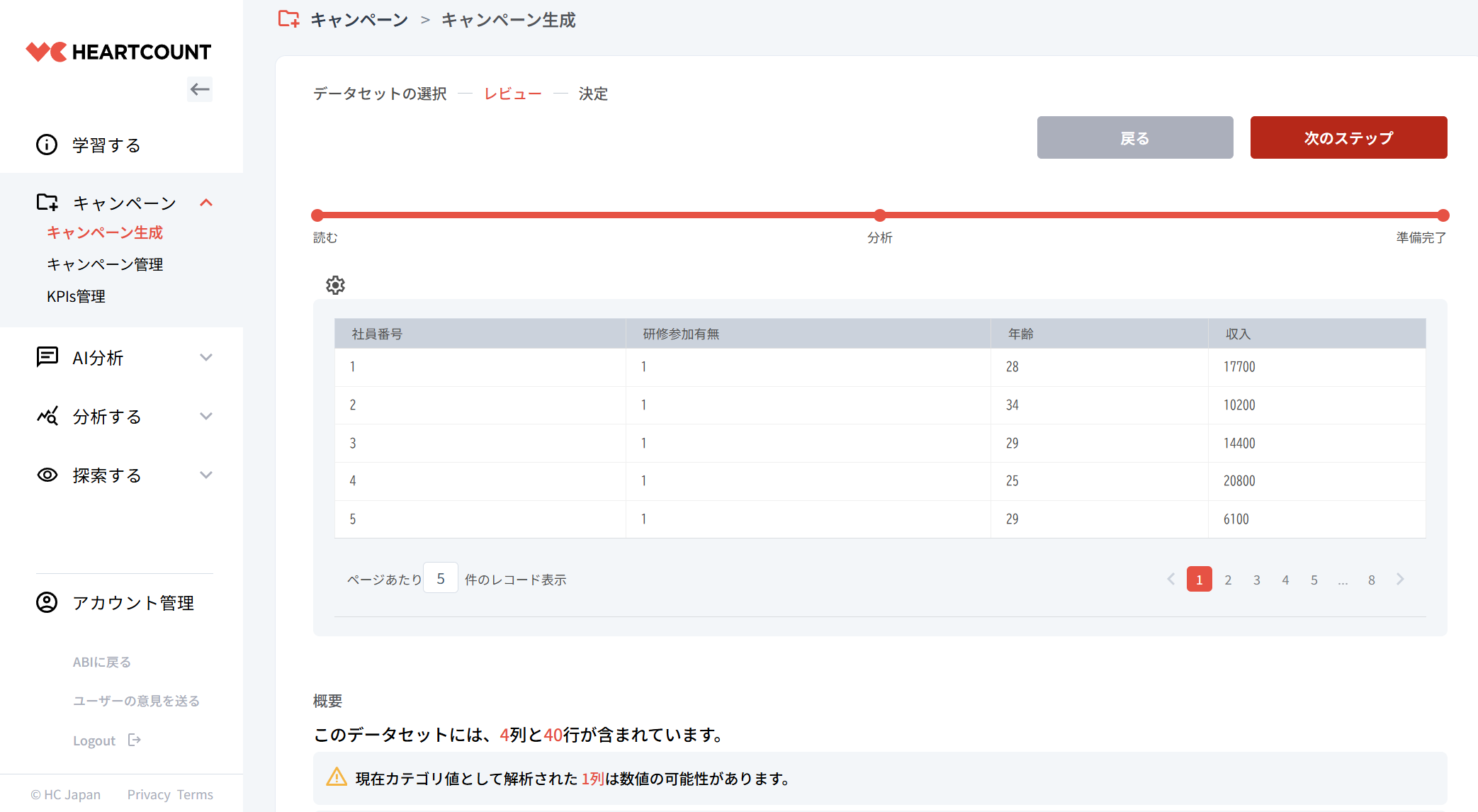
| 社員番号 | 研修参加有無 | 年齢 | 収入 |
|---|---|---|---|
| 1 | 1 | 28 | 17700 |
| 2 | 1 | 29 | 6100 |
| 3 | 1 | 25 | 20800 |
| … | … | … | … |
| 17 | 1 | 28 | 11500 |
| 18 | 1 | 27 | 10700 |
| 19 | 1 | 28 | 16300 |
そして、以下は研修を受けなかったグループです。
| 社員番号 | 研修参加有無 | 年齢 | 収入 |
|---|---|---|---|
| 20 | 0 | 43 | 20900 |
| 21 | 0 | 50 | 31000 |
| 22 | 0 | 30 | 21000 |
| … | … | … | … |
| 38 | 0 | 35 | 30200 |
| 39 | 0 | 32 | 17800 |
| 40 | 0 | 54 | 41100 |
しかしデータを見ると、研修を受けなかったグループの方が平均的に年齢が高く、年齢と収入の間の相関が交絡(confounding)を引き起こした可能性があります。
RCTの核心は、こうした変数が両グループに均等に分布するように無作為に割り当てる点にあります。サンプル数が十分に大きければ、年齢のように収入へ影響を与える要因も自然にバランスよく分布し、因果効果を正確に推定するための基盤が整います。
しかし前述の通り、現実的にはRCTを毎回実施するのは難しいため、それを代替できる方法が必要となります。
マッチング
マッチングの概念と方法
マッチングとは、文字通り似た特徴を持つ人同士をペアにして比較する方法です。
例えば、年齢28歳の社員番号1(研修参加)と社員番号27(研修不参加)を比較することができます。
このように、すべての年齢について可能なペアを見つけて比較すれば、年齢という変数の影響をコントロールした状態で研修の効果を推定できます。
こうした作業は、HEARTCOUNTのAI分析機能を活用すれば、手作業やコード作成を行わずに簡単に実践できます。
AI分析で実践する方法
1) データセットの準備
以下のデータをダウンロードします。
HEARTCOUNTでキャンペーンを作成 → ファイルを読み込み → 次へをクリックしてキャンペーンを作成します。
2) 基本比較
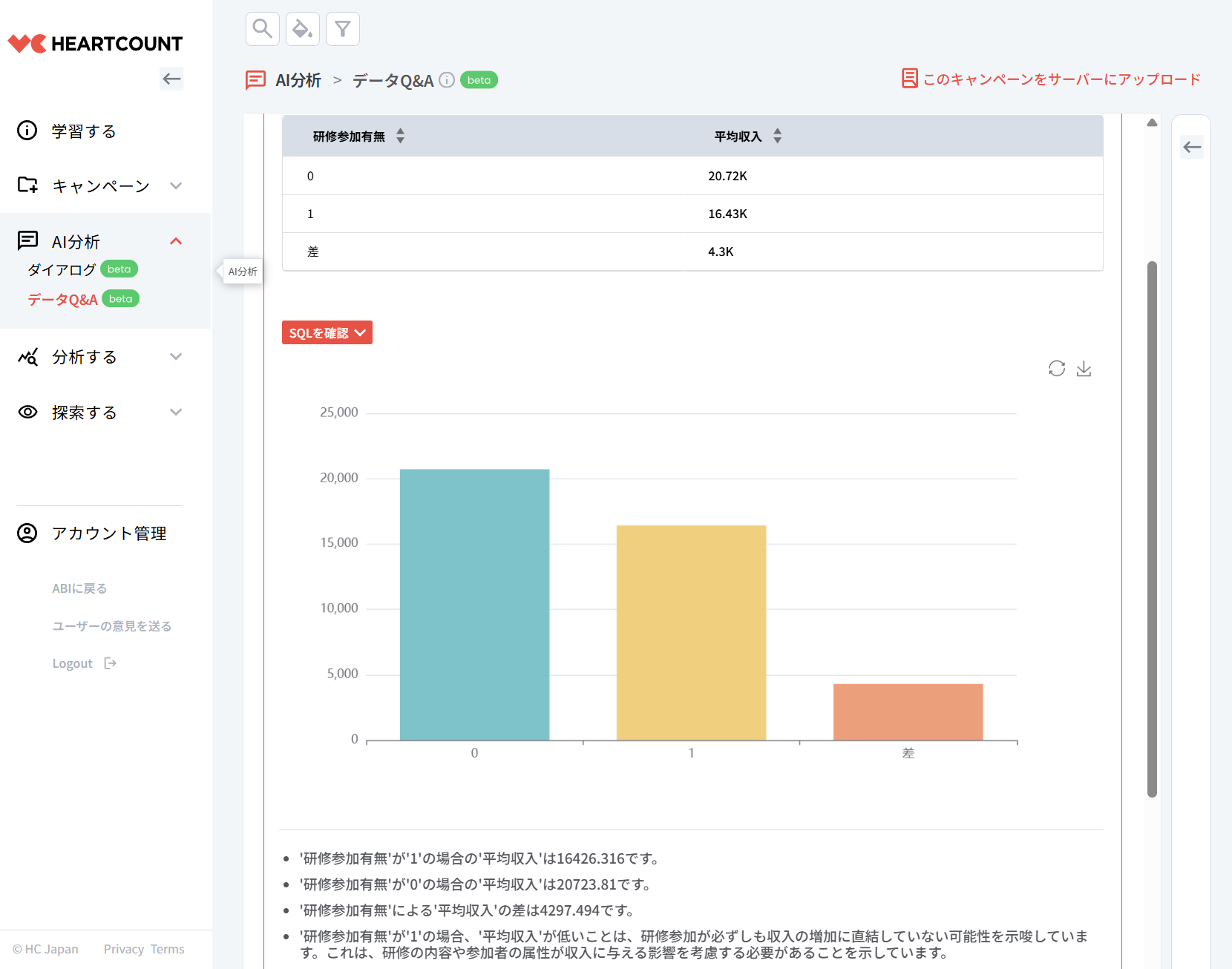
AI分析メニューの「データQ&A」機能を利用すると、自然言語で分析リクエストを行うことができます。自然言語の質問を入力すると、SQLクエリと可視化が自動的に生成されます。
研修参加有無ごとの平均収入を求めてください。そして、その差を教えてください。
3) マッチングによる比較
同じ「年齢」を基準に、「研修参加有無」が1の人と0の人をすべてマッチングし、各ペアの情報と「収入」の差を1行で表示してください。
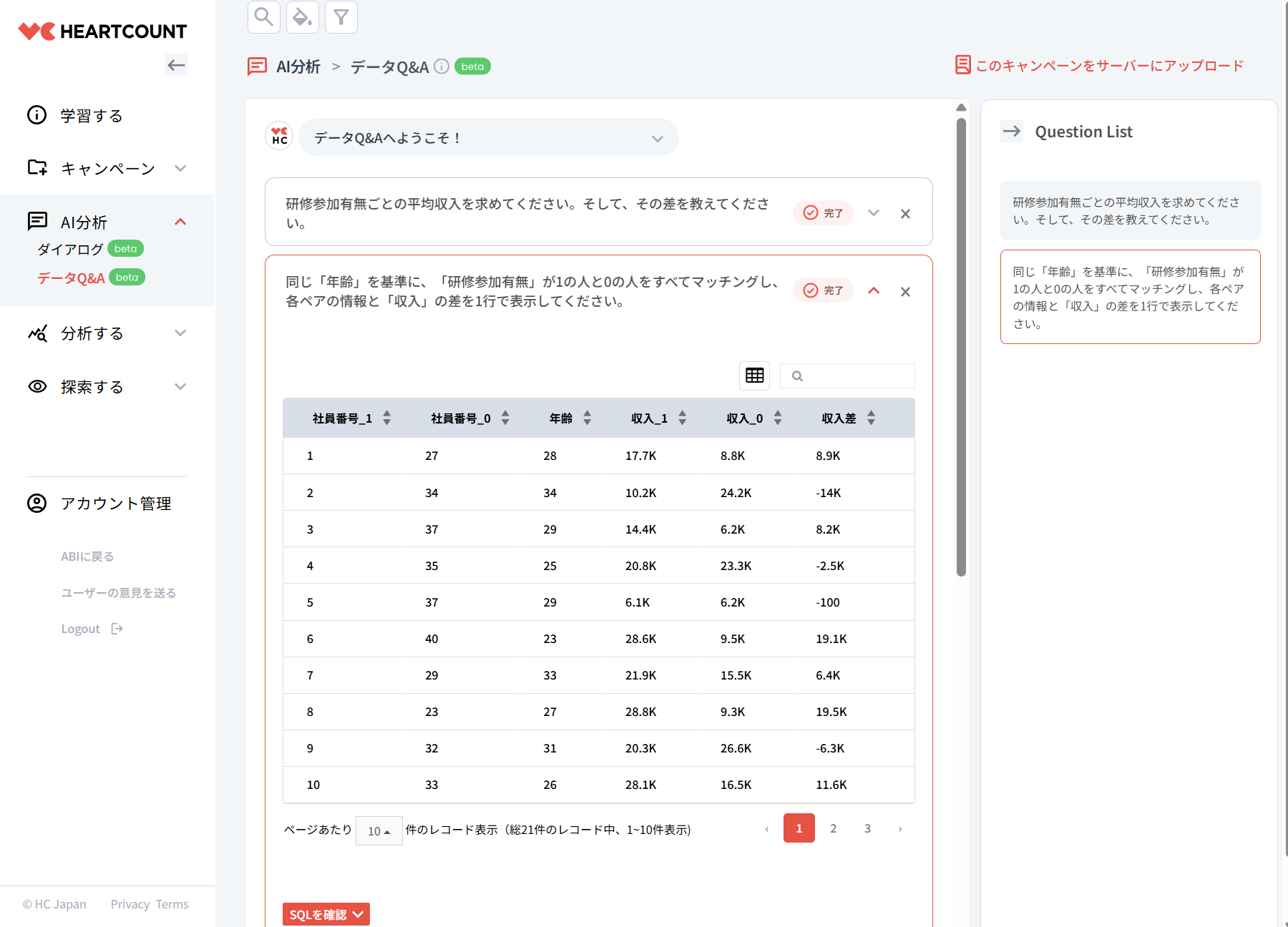
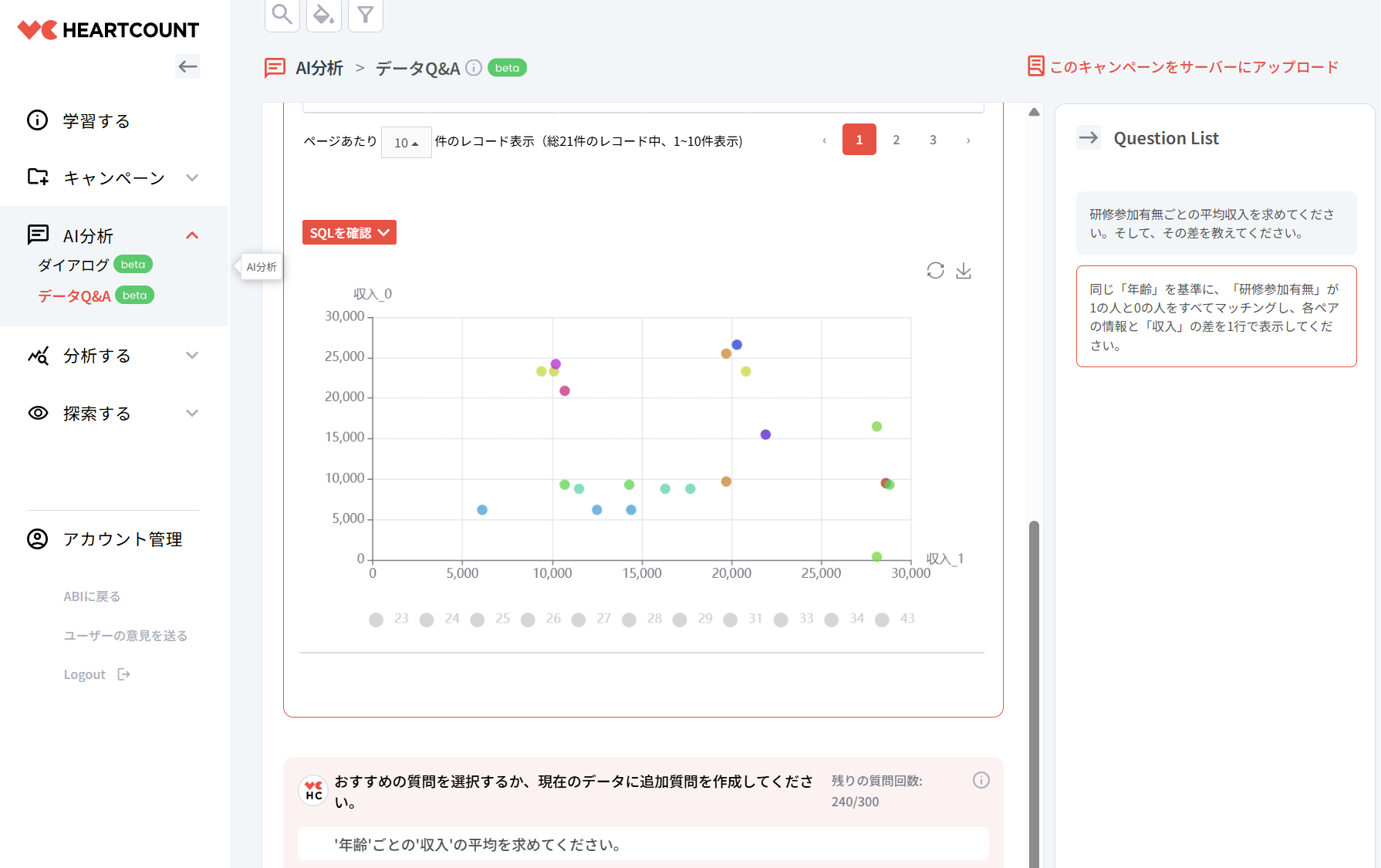
年齢を基準に適切にマッチングされていることが確認できます。これを基に効果を改めて推定します。
4) マッチングに基づく効果推定
同じ「年齢」を基準にマッチングされた「研修参加有」グループ(1)と「研修不参加」グループ(0)の「収入」差を計算し、その差の平均を算出してください。 結果は、参加者の平均収入、非参加者の平均収入、表形式で表示してください。
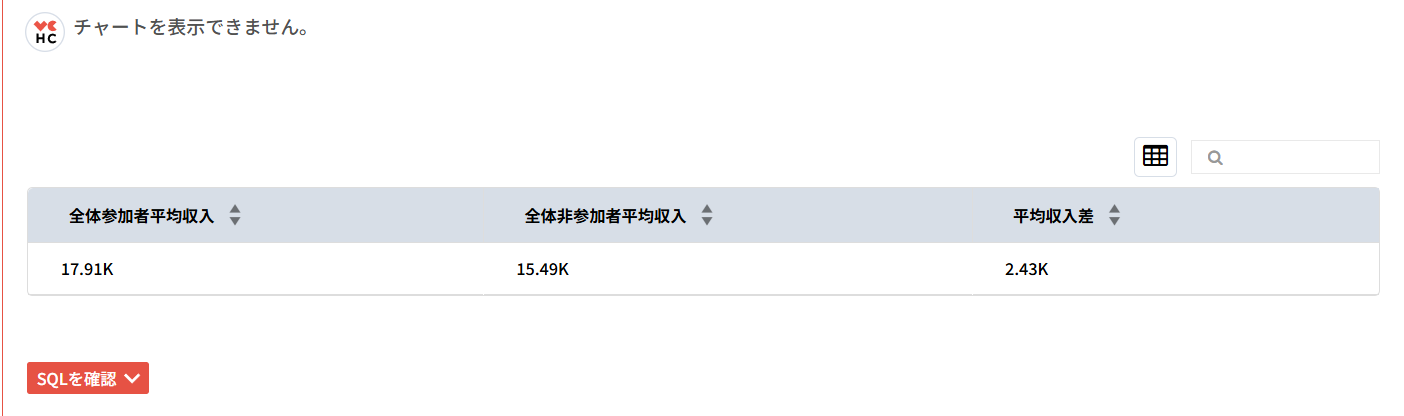
つまり、交絡因子(ここでは年齢)を統制すると、因果効果の推定が大きく変わり得ることが確認できます。
マッチングの限界と拡張
今回の演習では、単一変数(年齢)を基準にExact Matchingを行いました。しかし、実際の分析では、年齢だけでなく性別、職級、勤続年数など、さまざまな交絡変数(confounders)を同時に考慮する必要がある場合が多くあります。
このように考慮すべき変数が増えるほど、すべての条件を同時に満たすペアを見つけることが難しくなり、マッチング可能な標本数も急激に減少します。これを「次元の呪い(curse of dimensionality)」と呼びます。
その結果、多くの観測値が除外され、推定に使用される標本が母集団全体を十分に代表できなくなる可能性があります。つまり、私たちが求めた因果効果は、全体ではなく一部の小標本に限定された結果であるという限界が存在します。
これを補うために、CEM、PSM、IPTWといったさまざまな手法が用いられます。
RCTが困難な状況でも、観測データを活用して因果効果を推定する方法はいくつか存在します。マッチングはその一つであり、その後ほかの手法へと拡張していくことが可能です。
出典:
一緒に見ると参考になる記事:


![[因果推論1] Potential Outcome Framework (潜在的結果フレームワーク)](/ja/content/images/size/w540/2024/06/----------------------5.png)